
エクセルで作った軌道シミュレータver.3.1を全方向速度に対する空気力へ拡張しver.3.2にアップデートします。
数式は、ver3.0の抗力、ver3.1の揚力と同じ形の式をy,z方向速度についても拡張したものになります。
では式を立てます。少し長くなります。
軌道計算の運動方程式
ボールに作用する力を重量で割ると加速度が求まります。その加速度を時間積分すると速度になり、速度を時間積分するとボールの位置が求まります。
ボールに作用する力は「重力」、「抗力」、「揚力」の3つです。
[計算式]
x軸をホーム方向、y軸を一塁方向、z軸を上空方向と定義。
ボール回転軸は、z軸からx-y平面に向かう角度(真上から水平に向かう角度)をθs、x軸からy軸に向かう角度(ホーム方向から一塁側へ向かう角度)をΦsと定義。
今回は4シームとしてθs=110度、Φs=-80度とします。
ボール回転軸は、z軸からx-y平面に向かう角度(真上から水平に向かう角度)をθs、x軸からy軸に向かう角度(ホーム方向から一塁側へ向かう角度)をΦsと定義。
今回は4シームとしてθs=110度、Φs=-80度とします。
回転軸により揚力を各方向成分へ振り分けます。
抗力係数は暫定的に回転軸の向きによらず一定とします。
空気力による各方向への加速度
各方向の加速度を行列式でまとめて表すと以下のようになります。
各速度成分により発生する各方向への抗力、揚力をボールの重量で割ったものです。

ここで、sgn(dx/dt)はx方向速度(dx/dt)の向きを表す符号で、dx/dt>0(投手から
ホーム方向へ飛翔)ならsgn(dx/dt)=1, dx/dt<0(ホームから投手方向飛翔)なら
sgn=-1です。
二乗すると速度のプラスマイナスが分からなくなってしまうため、これを付けて区別
します。
例えば投手が投げるトップスピンのカーブと捕手が投げ返すバックスピンの球は、
三塁側から見ればどちらも同じ右回りの回転です。
しかしx方向速度が反対のため前者は下に変化、後者は上にホップと揚力の方向が反
対になります。
これを正しく再現するために速度のプラスマイナスの区別が必要となります。
Sgn(dy/dt), sgn(dz/dt)も同様です。
x方向

y方向
ここで、
v0:リリース時の球速、x0,y0,z0:リリース位置、
θ:上向きリリース角度、Φ:横向きリリース角度、t:リリース後経過時間
θ:上向きリリース角度、Φ:横向きリリース角度、t:リリース後経過時間
[計算式おわり]
ボールの空間位置x,y,zはtを代入すれば求まる形の式にできないため、エクセルで数値積分の方法で求めます。
具体的には、ti+1秒後の速度=ti秒後の速度 + ti秒後の加速度×(ti+1 - ti)、
ti+1秒後の位置=ti秒後の位置 + ti秒後の速度×(ti+1 - ti)、といった具合です。
エクセルへの数式入力
具体的には、ti+1秒後の速度=ti秒後の速度 + ti秒後の加速度×(ti+1 - ti)、
ti+1秒後の位置=ti秒後の位置 + ti秒後の速度×(ti+1 - ti)、といった具合です。
エクセルへの数式入力
では、エクセルへ入力していきます。
単位系はSI単位系です。
[エクセル入力]
まず初期条件を入力。
ver3.1と同様にしました。
ボールの回転軸角度は完全なバックスピンではなく、ジャイロ成分やサイドスピン(シュート)成分が混じっていることを考慮してθs=110度,φs=-80度とします。揚力係数CD、抗力係数CDの値は個人で計算や実測をするのが難しいのでネットで拾った値を使います。

次に時間tを少しずつ増加させて複数入力します。
ver.3.1と同じく、0.02秒おきにしました。
数値積分をするので時間間隔が小さいほど計算結果は正確になります。
そして時間t列のとなりに、d2x/dt、dx/dt、x、d2y/dt、dy/dt、y、d2z/dt、dz/dt、z用の列を9列挿入します。

X方向
dx/dt列の一番上のセルに、時間t=0における速度を入力します。(④式)

x列の一番上のセルに、時間t=0におけるx位置を入力します。(⑤式)

そしてd2x/dt2列に、dx/dtとdy/dtとdz/dtからd2x/dt2を計算する式を入力します。(①式)
再びdx/dt列に戻り、t>0のセルに数式を入力します。
②式の計算を数値積分で行うために下図のように数式を入力します。

再びx列に戻り、xのt>0について③式の計算を数値積分で行うために下図のように数式を入力します。

x位置の計算式はこれで完成です。
Y方向
dy/dt列の一番上のセルに、時間t=0における速度を入力します。(⑨式)

y列の一番上のセルに、時間t=0におけるy位置を入力します。(⑩式)

そしてd2y/dt2列に、dx/dtとdy/dtとdz/dtからd2y/dt2を計算する式を入力します。(⑥式)

再びdy/dt列に戻り、t>0のセルに数式を入力します。
⑦式の計算を数値積分で行うために下図のように数式を入力します。

再びy列に戻り、yのt>0について⑧式の計算を数値積分で行うために下図のように数式を入力します。

y位置の計算式はこれで完成です。
Z方向
dz/dt列の一番上のセルに、時間t=0における速度を入力します。(⑮式)

z列の一番上のセルに、時間t=0におけるz位置を入力します。(⑮式)

そしてd2z/dt2列に、dx/dtとdy/dtとdz/dtからd2yzdt2を計算する式を入力します。
重力加速度gも忘れないよう注意です。(⑪式)

再びdz/dt列に戻り、t>0のセルに数式を入力します。
⑫式の計算を数値積分で行うために下図のように数式を入力します。

再びz列に戻り、zのt>0について⑬式の計算を数値積分で行うために下図のように数式を入力します。z位置の計算式はこれで完成です。

完成です!

これで各時刻におけるボール位置x,y,zの値が計算できました。
[エクセル入力おわり]
では、計算されたx,y,z値を散布図でグラフ上にプロットします。
[エクセルグラフ化]
空気力(揚力、抗力)を全方向速度に対して完全に考慮した場合の軌道計算結果は、以下のようになりました。
グラフ中の点は0.02秒ごとのボール位置を表します。
グラフ中の点は0.02秒ごとのボール位置を表します。
空気力をx方向速度成分に対してのみ考慮し、y,z方向速度に対する空気力はなしとして計算しているver.3.1の軌道計算結果と重ねてみました。

しかし差が小さすぎてわかりません。完全に線が重なっており見分けがつきません。
ホームベース上における両者の軌道の差はわずか4mmです。
[エクセルグラフ化おわり]
ver.3.1のようにy,z方向の速度成分による空気力は省略しても、通常のピッチングにおける軌道計算をするなら十分な精度が得られるということです。
ここで行っている計算はエクセルで一瞬で終わるようなものなのでどちらでもよいのですが、サーバーでの計算時間が数百時間に及ぶような大規模シミュレーションではあってもなくても大差がない部分を上手く省略し効率化を図ることは重要です。
遠投軌道計算結果による影響比較
y,z方向速度成分による空気力あり、なしの場合の差が明確になるよう、遠投の軌道を計算してみます。
遠投では、ピッチングに比べボール軌道が山なりとなりz方向速度成分が大きくなりそれによる空気量の影響も無視できない程度に大きくなること、また飛翔時間が長いため空気力を受ける時間が長くなることにより、両者の軌道の差が顕著になります。
[計算結果2]
リリース角度を上向き35度に変更します。
それ以外の条件はピッチングの時と同様で球速140km/h、抗力係数CD=0.33、
揚力係数CL=0.20とします。
それ以外の条件はピッチングの時と同様で球速140km/h、抗力係数CD=0.33、
揚力係数CL=0.20とします。
ver.3.2ではボールが上昇していくときz方向速度に対しても抗力が働きより減速が大きいため、ver.3.1に比べ頂点の高さが6m程減少しています。
100m過ぎあたりのボールが落下していく段階では、ver.3.2方はz方向速度に対して揚力が働きまたz方向への落下速度に対して抗力のブレーキが働くため、ver3.1に比べるとやや水平に近い軌道になっています。
100m過ぎあたりのボールが落下していく段階では、ver.3.2方はz方向速度に対して揚力が働きまたz方向への落下速度に対して抗力のブレーキが働くため、ver3.1に比べるとやや水平に近い軌道になっています。
全体としては軌道前半の抗力による影響の方が大きく、ver3.2はver.3.1に比べ飛距離が10m減少しています。
(*) ver.3.2において140km/hでの飛距離115mは、実際と比べるとやや飛び過ぎているようです。今回使用した抗力係数CDの値0.33が、実際はもう少し大きいことが原因として考えられます。
(*) ver.3.2において140km/hでの飛距離115mは、実際と比べるとやや飛び過ぎているようです。今回使用した抗力係数CDの値0.33が、実際はもう少し大きいことが原因として考えられます。
[計算結果2おわり]
*****
今回でボールに作用する「重力」、「抗力」、「揚力(マグヌス力)」の3つの力を、全方向の速度に対して計算できる軌道シミュレータが完成しました。
加速度、速度からの時間積分を数値積分の方法で実行していますが、Microsoft Officeのエクセルや類似の表計算ソフトで簡単にできますので、よかったら作ってみてくださいね。
では、また。
(よかったら押してください。)
にほんブログ村

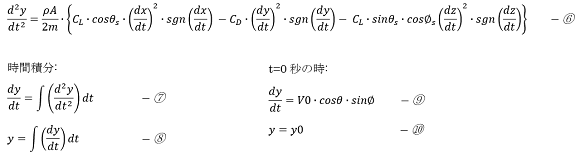







baseball savantから入手できるcsvデータで軌道シミュレーションをするにはどうすればいいでしょうか?
返信削除baseball savantのデータは、確か、球速、回転数、変化量のデータがあり、回転軸のデータがなし、だっと思います。 その場合は計算結果の変化量がデータ値と一致するよう、軌道シミュレーターにインプットする回転軸θs,φsの値を調整してやれば第43-49回みたいな感じで軌道を再現できます。
返信削除これのバッティングバージョンはどこに載ってますか?他記事を読んだのですが、同じ計算条件を入力してもグラフが出来ません。エクセル初心者なのですが、何か間違っているところなどがありますのでしょうか?
返信削除バッティングもこれと同じので計算してます。
削除グラフできないとのことですが、確認方法としては入力値を変えて傾向通りになるか試してみるとよいと思います。例えば球速を上げると飛距離が伸びるとか、θをプラスで大きくすると上向きに飛んでいくとか。
昨日質問させていただいた者です。このグラフの表し方が分かりません。散布図を作っても、yとzについてのグラフが出てきてしまい、この図の様に、全てが一つに合わさったグラフが作れません。このグラフはどうやって作ればいいのか教えてもらってもいいでしょうか。初心者で全く無知なので、非常に曖昧な説明で申し訳ありません。
返信削除エクセルの操作は、グラフを左クリックで選択>右クリック>データの選択>編集>系列Xの値、に横軸にしたいデータを選択>OK>編集>系列Yの値、に縦軸にしたいデータを選択>OK>OK、です。上のピッチングのはグラフを3つ作ってます。
削除何度も重ね重ね質問申し訳ございません。rpmの計算は、数式のどこに入れればいいのでしょうか?
返信削除rpm(回転数)は直接入力しないです。回転数に応じた揚力係数CL、抗力係数CDを入力します。
返信削除CL、CDの値は求めるのがとても大変で個人でエクセルでできるような規模ではないため、拾ってきた値を使います。
例えば下記のようなものです。
https://www.fit.ac.jp/~mizota/pdf/ronbun2011_05.pdf
もし大学生の人でしたら、論文を当たって信頼性のあるものを引用するのがよいと思います。
以下補足で、CLとCDはスピンパラメータSp=π×回転数/球速によって変わります。Spを計算するときの単位は回転数がrps(一秒間当たりの回転数)で、球速はm/s(秒速xxメートル)であり、なじみのあるrpm(一分間当たりの回転数)やkm/h(時速xxキロメートル)でないことに注意が必要です。
コメント失礼いたします。
返信削除今回の記事の式について正確性を問いたいのですが、球の空力特性にはレイノルズ数も関係してくると思うのですが、考慮されているのでしょうか?
コメントありがとうございます。
削除このシミュレータは抗力係数CD、揚力係数CLの値をインプット値として軌道を計算するものであり、CD,CLの値を求めることはできないので、対象とされているRe数でのCD,CLの値は論文などから引用されることをお勧めします。
コメント失礼いたします。θsとφsについてですがφsの角度がよく理解できないのですが、アドバイスとして何か詳細を教えていただけませんか?
返信削除上と同じ方かな?θsとφsは数学や物理学で使われる一般的な球座標の定義になっています。wikipediaで球面座標系で検索してもらうと図がでてきます。
削除最初に回転軸がZ軸と一致(真上から見てボールが反時計回りの回転)していて、そこからθsだけX軸方向(ホーム方向)に傾きます。そのあとΦsだけy軸方向(一塁側)に傾きます。
これ分かりづらいですよね、ラプソードみたいに定義すればよかったなって思ってます。
揚力と抗力の向きですが、ボールの進行方向と垂直の方向に定義されていますか?それとも、ホーム方向と垂直の方向に定義されていますか?
返信削除ボールの進行方向に合わせています。
削除