
エクセルで作成した"軌道シミュレータver3.1"を使ってカーブ、フォークの軌道を計算し、4シームの軌道と比較します。
カーブの軌道
まずはカーブです。
カーブは重力と回転によるマグナス力(揚力)の両方により下方向へ変化します。
4シームが重力による落下をマグナス力で打ち消し直線に近い軌道になるのとは対照的に、カーブは大きく弧を描く軌道となります。
[計算条件]
カーブ
球速 v0=120[km/h]、リリース角度 θ=0度(水平)
リリースポイント x0=1.8m(ホーム方向)、y0=-0.5m(三塁方向)、z0=1.8m(高さ)
ボール回転軸角度 θs=60度、Φs=45度
抗力係数 CD=0.43、揚力係数CL=0.27
4シーム
球速:v0=140[km/h]、リリース角度:θ=-3度(下向き)
ボール回転軸角度 θs=110度、Φs=-80度
抗力係数 CD=0.40、揚力係数CL=0.20
ボール回転軸

θs : z軸からx-y平面に向かう角度(真上から水平に向かう角度)
φs : x軸からy軸に向かう角度(ホーム方向から一塁側へ向かう角度)
[計算条件終わり]
[計算結果]
ボール軌道の計算結果は以下のようになりました。
グラフ中の点は0.02秒ごとのボールの位置を表します。
カーブの方が4シームよりも3度上向きにリリースされているため、投げた瞬間は4シームよりも高い位置を通過する軌道になります。
その後徐々に下方向へ変化を始め、14mあたり、ストライクゾーンの4m手前になってようやく4シームの軌道より下に行きます。
そこから残りの4mで両者の差はぐっと大きくなります。ストライクゾーンを通過するときには4シームが低めいっぱいであるのに対し、カーブの軌道は30cmほど下を通過しホームベースの後ろでバウンドします。
打者からすると、投げた瞬間は高めのボール球なので振るのを止めようと思ったのが、下に変化しストライクになりそうなので慌てて振ったら、低めのボール球でしまったという感覚になるでしょう。

下方向に加え、横方向へも大きく曲がっています。ストライクゾーンからボールゾーンへ逃げています。振らせることができれば空振りが取れそうなコースですが、8メートル過ぎから4シームの軌道との差が大きくなっているので目の良い打者には見切られるかもしれません。
[計算結果おわり]
フォークボールの軌道
次はフォークボールです。
フォークボールは回転数が小さいためマグナス力(揚力)がほとんど作用せず重力によって落下します。
4シームが重力による落下をマグナス力で打ち消し直線に近い軌道になるため、それと比べてフォークボールは下方向に変化するような軌道となります。
[計算条件2]
フォーク
球速 v0=120[km/h]、リリース角度 θ=-2度(下向き)
ボール回転角度 θs=110度、Φs=-80度
抗力係数 CD=0.38、揚力係数CL=0.07
4シーム
球速:v0=140[km/h]、リリース角度:θ=-3度(下向き)
ボール回転角度 θs=110度、Φs=-80度
抗力係数 CD=0.40、揚力係数CL=0.20
[計算条件2終わり]
[計算結果2]
ボール軌道の計算結果は以下のようになりました。
フォークボールのリリース角度は4シームよりも1度だけ上向きですが、投げた瞬間の軌道はほぼ重なっています。
その後徐々に下方向へ変化を始めますが、12mあたりまでは4シームの軌道とほとんど差がありません。
そこから両者の差は広がり、ストライクゾーンを通過するときには4シームが低めいっぱいであるのに対し、フォークボールの軌道は35cmほど下を通過しホームベースの上でバウンドします。
打者からすると、投げた瞬間は低めのストライクなので思い切り打ってやろうとしたら、ストライクゾーンの5メートル手前から落ち始めて慌てバットを止めようとしたが、止まらずに空振りしてしまった、という感覚になるでしょう。

x-y平面のグラフを見ると、4シームがシュート成分によりわずかに横方向へ曲がっているのに対し、フォークボールではマグナスが働かずほぼ直線軌道となっています。両者の横方向変化量の差は12cm、ボール1個半程度です。
フォークボールはアウトコースいっぱいを狙わず真ん中低めのストライクゾーンから落とす方が空振りをとれると言われていますが、この横方向の変化量の違いが関係しているのかもしれません。
[計算結果2おわり]
カーブ軌道の3D動画
エクセルには3Dプロット機能が備わっていないようです。
代りにRinearnGraph3Dというフリーソフトを使って軌道を3Dプロットし、それをgifで動画ファイルにしてみました。
一コマ0.02秒で実際のスピードと同じにしてあります。
視点は左打席からのものをできる限り再現してみました。
[3Dプロット動画]
4シーム
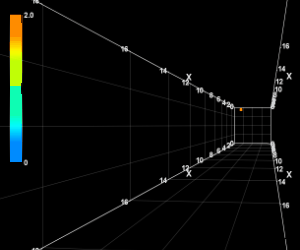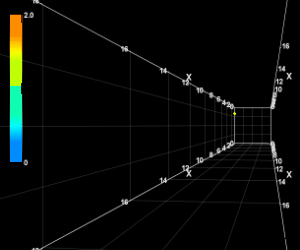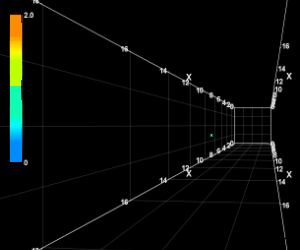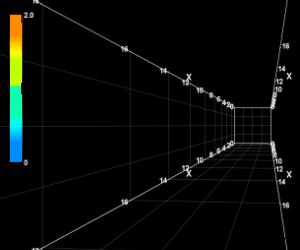
カーブ

では、また。



参考になった
返信削除それはよかった。(^▽^)
削除