食い違い
野球でホームランを狙ったり、遠投で記録を測る際はできるだけボールの飛距離を大きくしようとします。そのためには球速やバックスピン回転に加えて、打ち出す、あるいは投げ出すときの上向き角度もまた重要です。
トラッキングデータによれば、上向き30度のとき最も飛距離が大きくなり、ホームランが出やすいという傾向があります。
そういうと、「あれ、45度じゃないの。そう習ったけど。」と思う人が、いるかもしれません。
確かに、高校物理の教科書を見ると、45度のとき飛距離が最大になると書かれています。
この食い違いは一体なんでしょうか。どちらが正しいのでしょうか?
どちらも
トラッキングデータは実現象を測定した結果なので、正しいです。
また教科書は確立、検証がきちんとなされた物理学の計算式に基づいており、正しいことが書かれています。
結局のところ、これはどちらも間違っておらず、どちらも正しいです。ただ、条件が異なるだけです。
高校物理の教科書を見ると、必ず「ただし、空気抵抗は無視できるものとする。」との一文が添えられています。空気抵抗がない場合、45度が飛距離最大になります。(細かいことを言うと、これは発射位置と落下位置の高さが同じ場合です。)
しかし、大気中を高速で飛んでいく野球ボールは、無視できないほどの空気抵抗を受けます。ブレーキとして働く抗力と、回転により軌道を曲げようとする揚力です。
この空気抵抗を受ける場合は、30度が飛距離最大になります。(細かいことを言うと、これは適度なバックスピン回転で上向き揚力が作用する場合です。)
空気抵抗の有無により、飛距離を大きくするための最適角度は変わってくるわけです。

45度が最大になる理由
空気抵抗が無視できる場合、なぜ45度で飛距離が最大になるのでしょうか?
詳細な説明は教科書を見れば書かれていますので、結論だけ言うとθ=45度のとき、sin(2θ)が最大値をとるからです。
球速vの垂直成分v・sinθが大きいほど、重力で地面に落ちてくるまでの時間が長くなります。
また水平成分v・cosθが大きいほど同じ時間内で前に進む距離が大きくなります。
この2つが大きいほど飛距離は大きくなるのですが、θが大きくなるほど前者のsinθが大きくなるのに反して、後者のcosθは小さくなります。一方が大きくなると、もう一方が小さくなってしまうのです。
両者がどちらもそれなりに大きく、最も飛距離が大きくなる角度を探すと、水平と垂直のちょうど中間の45度、というシンプルな答えになります。(これは四角形の周囲の長さが一定のとき面積最大となるものを探すと、縦横の長さが同じ正方形という単純な答えにいきつくのと似ています。)
飛距離Lの式を数式で書くと以下のようです。
L = 2・v^2・cosθ・sinθ / g
= v^2・sin(2θ) / g -①
(v:球速、θ:上向き角度、g:重力加速度)
空気抵抗が無視できる条件
さて、この地球上どこへ行っても空気は存在します。
では、「空気抵抗は無視できる」という条件下での飛距離計算式①は、テストで点をとるためだけのものであり、現実世界の現象を計算するのには全くの役立たずでしょうか?
というと、そこまでひどいものではありません。空気があっても、その影響が、重力による影響よりもずっと小さく無視できるならば、十分な近似として有用です。
どのような場合に空気抵抗を無視できるかと言うと、大きさのわりに重たいものを、遅い速度で飛ばす場合です。
重力。慣性と力のmは打ち消し合う
ボールの重量が145gである、と聞いた時、物理学を学んだ人は2つのものを思い浮かべます。
重力質量
一つは「重力質量」です。重力により下に引っ張られる力はこれに比例します。145gのボールには1gの一円玉よりも強い重力が働き、100kgの鉄塊よりも小さい重力が働きます。重力質量が大きいためです。
重力質量は、式で言うと
P=m・g
(P:重力、m:重力質量、g:重力加速度)
のmです。
慣性質量
もう一つは「慣性質量」(あるいは「力学質量」)です。外から力を受けたときの、運動の変化のしにくさを表します。145gのボールは片手でも加速できますが、100kgの鉄塊は両手で強く押しても全然加速されません。慣性が大きいためです。
慣性質量は式で言うと、
F=m・a(F:外力、m:慣性質量、a:加速度)
のmです。
重力を受ける運動において、ボールにかかる重力は重量質量mに比例して大きくなり、一方力を受けたボールの加速度は慣性質量mに反比例して小さくなります。幸いなことに、物理学の先人たち、エートベッシュやディッケなど、により両者の質量mは全く同じであることが確かめられているため、分子と分母のmは打ち消しあい、その結果重力を受けるボールの動きはその重量に関係なく同じになります。重量が大きいものは強い重力を受けますが、それと同じ分だけ慣性が大きく力を受けた時に加速されにくいため、依存しなくなるわけです。
上記の飛距離の計算式(①式)に、ボール重量(質量)mが出てこないのはこのためです。
空気力。∝1/m
空気抵抗によって受ける力、空気力はどうでしょうか?
ボールが受ける空気力の大きさはボール重量には無関係です。球速、断面積(直径)、回転などが影響します。
慣性(外から力を受けた時の運動の変化のしにくさ)は、先述のようにボール重量mに反比例します。
そのため、球速vが遅く、ボール重量mが大きいほど空気力による加速度は小さくなります。これが重力による加速度よりも2桁、3桁と小さければ「空気抵抗を無視」することができます。
遅くて、重いもの
野球のボールは100km/hを越える高速であり、重量がそれほど大きくないため、空気の影響をしっかりと受けます。
低速かつ重量が大きく、空気抵抗が無視できるようなものは何があるでしょうか?
真っ先に思い浮かぶものは、砲丸投げの砲丸です。しかも砲丸投げは飛距離そのものを競う競技です。今回のテーマにうってつけです。
バスケットボールも低速かつ重量大ですが、試合で飛距離を重視するスポーツではありません。
というわけで、今回は砲丸投げでは45度で飛距離最大になるのか、軌道計算を行います。

砲丸投げ、45度と30度の軌道計算
同じ条件で、リリース時の投てき上向き角度を45度と30度にした場合の軌道計算をし、その飛距離を比較します。
[計算条件]
球速はトップクラス選手を想定した45km/hとします。抗力係数CDは球体の一般値0.40を、揚力係数CLは砲丸投げでは押し出すようにして投げ回転がほとんどかかっていないことから0とします。
[計算結果]
上向き45度と30度で投てきした場合の、砲丸の軌道計算結果は以下のようになりました。
0.05秒ごとの砲丸の位置をプロットしています。
陸上選手は40度弱
角度と速度
砲丸投げ、40度、球速アップの軌道計算
砲丸投げにおいて45度から40度に、5度投てき角度を下げることによりどれくらい球速が上がるのかはデータがなく不明です。そのため今回はそれほど大きくなく、キリが良い値として、仮に1km/hアップするとします。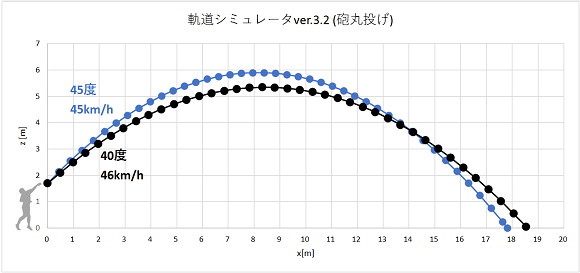
40度、46km/hでの飛距離は18.6メートルとなりました。
45度、45km/hの場合を78cm(=(18.6-17.8)×100)上回りました。
わずか1km/hの違いのわりには大きな飛距離の差です。
また40度の方が飛距離が大きくなったのは、リリース位置よりも地面の方が低い位置にあることも影響しています。リリース位置と同じ高さまで落ちてきた後から地面に落ちるまでの間に関しては水平方向の速度成分が大きい方ほど飛距離が増えるため、投てき角度が低い方が有利になります。
というわけで、砲丸投げにおいて飛距離最大にするためには、空気抵抗を無視できかつ球速一定の場合の最適角度45度をベースにし、そこから少しずつ角度を下げていき実際に飛距離最大となる最適角度を探していく、と言うのがベストな解になります。
*****
村田兆治さんと落合博満さん。
ロッテで活躍した二人のレジェンドは、少年期に砲丸投げをやっており、それが軸足に体重を乗せて運ぶ独特のフォームとなって活かされました。
3キロのウエイトボールを砲丸投げのように投げることを繰り返すと、下半身の力を手に伝える感覚が養われます。さらに全身の筋力アップにもなるので、お勧めのトレーニングです。
では、また。
















