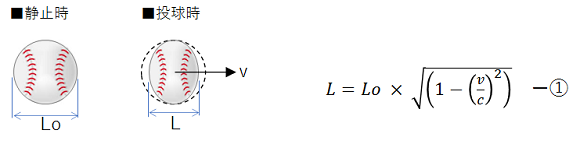第127回 150km/hの時間旅行

2つの相対論

物理学の相対性理論には、特殊相対性理論と一般相対性理論の2つがあります。

大雑把に言うと特殊相対性理論は、光速に近い速度で移動する物体は①進行方向に縮み、②時間の進みが遅くなり、③質量が増加するというものです。

実世界の現象でありながら、日常生活における常識が覆される面白さがあります。

一般相対性理論は、特殊相対性理論を発展させたもので、重力を取り扱います。

720万分の1

特殊相対性理論の影響が出てくるは、速度が光速に近い時のみです。

光の速度は、秒速30万キロメートルです。

それに対し野球の投球は150km/hほどで、これは秒速42メートルです。

これは光速の1/7200000(=42/300000000)です。7桁小さいオーダーです。

つまり、野球の話をするとき相対性理論の適用は不要です。

不要ですが、面白そうなので、今回は野球ボールに相対性理論を適用するとどうなるのか、計算をしてみます。

野球ボールのローレンツ収縮の計算

相対性理論に従えば光速cに近い速度で移動している物体は、静止している人(静止系)から見て移動方向の長さが縮んでいるように見えます。

野球の投球ならホーム-センター方向にボールがつぶれて縦長の楕円形に見えるということが起こります。

空気抵抗などの"力"を受けて変形しているのではなく、"時空"が縮むことにより時空の中に存在するボールも一緒に縮みます。

この現象を「ローレンツ収縮」と言います。

ローレンツは物理学者の名前です。

相対性理論といえばアインシュタインですが彼の完全な独力でつくり上げられたものではなく、先人達の仕事から多くのヒントを得ています。ローレンツの他にも、ポアンカレ、マッハ、マクスウェル、マイケルソンとモーレーなどが大きな影響を与えています。

ローレンツ収縮の計算式は①式のようです。

この式は三平方の定理から導かれ、誰でも計算できる形をしています。

興味を持って訪れた人にいきなり難解な数式をぶつけて門前払いしてしまわないのも、相対性理論の良いところです。

物体の速度vが光速cよりもずっと小さいときv/c≒0なので、①式のルートの部分がほぼ1となり、L≒Loとなり、ローレンツ収縮の効果がなくなります。

そのため物体の速度vが光速cに比べずっと小さいとき、相対性理論の適用は不要となります。

それでは、どれくらい縮むのか（縮まないのか）計算してみます。

[計算結果]

球速vはメジャーリーグの4シームを想定し、150km/hとします。

①式の計算結果は以下のようです。

球速150km/hの投球は、ローレンツ収縮により7×10^-13mm、前後方向に縮みます。

桁が小さすぎてどのくらいなのか良く分かりませんね。

他のものと比べると、7×10^-13mmは、電子(古典電子半径 2.8×10^-15m)の大きさの1/8程度です。

肉眼で見て縮んでいるのが分かるようなレベルではありません。　

割合で言うと、元の径の0.99999999999999倍に縮みます。小数点の後ろに9が14個も並びます。パーセントで言うと、99.999999999999%です。お酒やドラマの名前がこんなに長ければ、消費者はうんざりしてしまいます。

それでもプランク長さよりは長いため実際にボールは収縮しています。

野球ボールの時間旅行の計算

次は、時間の遅れです。

映画「猿の惑星」ではラストで(※ネタバレ注意）主人公が未来の地球へタイムトラベルしていたことが明らかになります。

相対性理論では光速に近い速度で移動しているものは時間の流れがゆっくりになるため、宇宙船が地球に対して光速近くまで加速していたとすればあり得る話となります。

野球ボールでも、例えば小さな虫がボールに貼り付たまま投げれば、虫は時間旅行をします。キャッチャーミットで受け止められた時までの時間進みの遅さの分だけ、虫にとってグラウンド上の人達は早く時間が進んでいるので、未来の世界に到着することになります。

この虫がどれだけの未来へ時間旅行するのか計算してみます。

時間の遅れの計算式は上図②式のようで、先ほどのローレンツ収縮と同じ形をしています。

[計算結果]

球速vは先ほどと同様に150km/hとします。投げてから捕るまでの飛行時間は0.45秒とし、加速と減速にかかる時間は無視します。

②式の計算結果は、以下のようです。

球速150km/hの球に貼り付いた虫は、4×10^-15秒だけ未来へ時間旅行をします。

これも桁が小さすぎて良く分かりません。

光は1秒間に地球7周半分の距離を進みますが、4×10^-15秒の間ではわずか千分の一ミリしか進めません。それだけの短い時間です。

それでもプランク時間よりは長い時間のため実際に時間旅行は起こっています。

10^-15秒の時間遅れでは、例え何万、何億球投げようとも、この虫が22世紀まで長生きすることはできそうもありません。

それどころかむしろ空気中で音速を超えるときの衝撃波や、摩擦による熱のダメージで寿命を縮めてしまうことでしょう。

またボールの時間遅れはこのように極めて小さいため、速球王の中に仕込まれたストップウォッチを相対論に基づいて補正する必要はありません。

　

野球ボールの質量増加の計算

最後は質量の増加です。

「質量はエネルギーと等価」というフレーズおよび「E=mc^2」の式は、相対性理論の中でも最も有名な部分の一つです。

アインシュタインを尊敬する人は彼のおかげで原子力発電ができたと称え、そうでない人は彼のせいで核兵器が生まれたと非難します。世界が平和になりますように。

投手の投げた野球ボールは運動エネルギーの分だけ静止時より多くのエネルギーを持っており、その分だけ質量mが増加します。

質量増加の計算式は上図③のようです。これもまたローレンツ収縮と同じ形の式をしていますが、質量は増える方向なのでルートの部分で割る形になります。

では、どれくらい質量が増加しているのか計算してみます。

[計算結果]

球速vは先と同様に150km/hとします。ボールの静止質量は0.145kgとします。

③式の計算結果は以下のようです。

球速150km/hの投球は、質量が1×10^-15kg増加します。

これもやはり桁が小さすぎ、良く分かりません。

他のものと比べると、人の細胞一個の中にあるDNA(3×10^-15kg)の1/3程度です。

割合で言うと元の質量の1.00000000000001倍、100兆分の1倍だけ増加します。

これだけわずかなので投手がリリースの瞬間に「ボールが重くなった」と感じることはありません。

もしそう感じたとしてもそれは相対性理論の効果による質量増加ではなく、加速時の慣性力です。ボールを押した分だけ手が押し返される「反作用」の力です。

第126回 ヘッドスライディングvs足スライディング。どちらが早いか？

 

ヘッスラvs足スラ

ヘッドスライディングと足からのスライディング。

どちらがより早くベースに到達できるだろうか？

一般的にはヘッドスライディングのほうが早いというイメージを持たれているようである。

物理学的な観点からは、ベースに触れる部分が体の重心から離れている方が有利だと言える。

重心から足裏までの距離L1と、万歳をした時の重心から手先までの距離L2を比べ、L1>L2なら足スライディングのほうが早い。L2>L1ならヘッドスライディングのほうが早い。

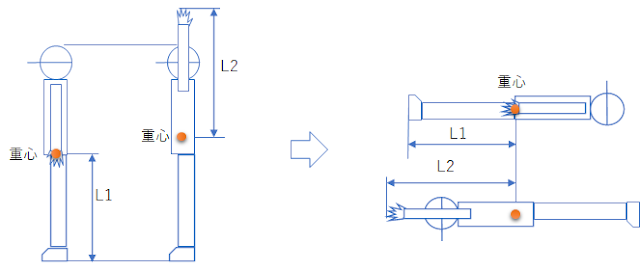図1

スライディングするとき、地面をけり体が宙に浮くともはや足からの力で体の重心を加速することはできなくなる。

どちらのスライディング方法でも重心の動きが変わらないのであれば、ベースに触れる部分が重心から遠いほど、ベースに触れる部分はよりベースに近くなり、早くベースに触ることができる。

数値で比較

図1のポンチ絵ではL2がL1よりかなり大きいが、実際にはそこまで差はない。

数値を計算してみる。

直立姿勢での足裏から重心までの距離L1は身長のおよそ6割であるため、180cmの選手ではL1=110cmほどである。

手を上に挙げたときの足裏からの距離は身長のおよそ1.2倍であるため、180cmの選手では220cmほどである。これからL1を引けばL2=110cmとなり、L1とほぼ同じである。

手を上に挙げると腕の重量分だけ重心が頭の方へ移動することを考慮すると、L2はこれよりも少し小さくなる。

L1>L2となる。

そのためヘッドスライディングは足スライディングよりも早いとは言えない。

加えてプロ野球選手は一般人よりもスタイルが良く、足が長く重心位置が高いため、L1が大きい。

そのため足スライディングのほうがやや早いと考えられる。

調査報告

実際に1塁から2塁までの到達時間をリトルリーグ、高校、大学の選手で調べた報告がある。

どのレベルでも「同じか、足からのスライディングのほうが早い」という結果がでている。(*1)

ヘッドスライディングはケガをしやすい上に、早くならないのである。通常は足スライディングをするのがよい。

ヘッドスライディングをするメリットは、足より自在に動く手でタッチをかいくぐれることである。左手を前に出しておき、タッチが来たら引っ込め右手で三塁ベースを触るテクニックはプロ野球でも成功例がみられる。

また牽制球の帰塁時は、速度がゼロの重心を足で加速しながらスライディングする必要があるため頭から戻る。

(*1) 参考文献：BBMスポーツ科学ライブラリー 科学する野球 バッティング&ベースランニング　平野裕一著　ベースボール・マガジン社

ヘッスラvs駆け抜け

ちなみに上記の参考文献によると、内野ゴロで打者走者が1塁へ走るときについても調べられている。

結果は「ヘッドスライディングより駆け抜けた方が早い」、ただし「スライディング距離を短くして1塁のやや右へヘッドスライディングすれば、駆け抜けよりも早いが、けがのリスクも高まる」とのこと。

うまくやればヘッドスライディングのほうが早くなる可能性はあるが、10・8の立浪監督のようになるリスクのほうが高い。

一塁へのヘッドスライディングはチームメイトの精神を高揚させ、士気を上げる効果もあるが、けがしてしまってはそれも叶わない。

ヘッドスライディングのコツ

ヘッドスライディンで早くベースに到達するためコツは、重心から手先までの距離L2が大きくなるような姿勢をとることである。

そのためには足の膝から先を後ろへ、真っすぐ伸ばせばよい。膝下の重量分だけ重心が手と反対方向へ移動しL2が増加する。

図2

守備でダイビングキャッチをするときも同様である。

足を真っすぐ伸ばすことで、グラブをボールに近づけることができる。名手のダイビングキャッチを美しいと感じるのは、手足がきれいに伸ばされているからである。

またバレーボールではスパイクを打つ選手も、それをブロックする選手も足がまっすぐ伸びている。ネットを挟んだ敵同士の選手が同じような姿勢をとる。足を真っすぐ伸ばし重心を体の下の方へ移動させることで、同じ重心の高さでもL2が大きい分、手の位置を高くすることができる。

足スライディングのコツ

足からのスライディンで早くベースに到達するためコツは、重心から足先までの距離L1が大きくなるような姿勢をとることである。

そのためには上半身を後ろへ倒せばよい。上半身の重量分だけ重心が足先と反対方向へ移動しL1が大きくなる。

図3上のポンチ絵のように完全なあおむけでは背中が地面と接し摩擦によりブレーキがかかるし、前が見えないので、実際は少し起こす。

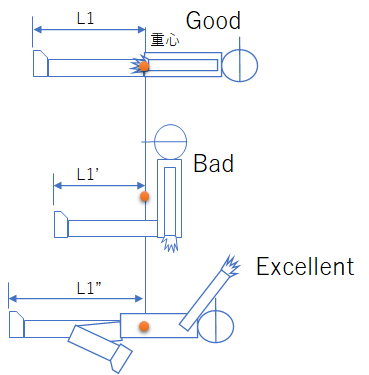図3

両手を上に挙げると手の重量分だけ重心は足先から遠ざかるので、なおよい。岡林選手のように、あおむけでなく、体を横向きにするタイプは片手を地面に擦るようにして足先から遠ざけるとよい。

またベースに触れないほうの足の膝を曲げると、これによっても重心が遠ざかるのでよい。

言われなくても選手は皆そうしており、滑り台のように両足を前に伸ばしてスライディングする人は見たことがない。

次の塁を狙うために

余裕でセーフのタイミングならば上半身は深く倒さず、図3中のように少し起こした姿勢の方がスライディング後に素早く立ち上がれるので、むしろよい。

重心の位置が高いため、ベースに触れる足先との高低差がモーメントアームとなり、図で左回りのトルクが発生するためである。

また可能ならば右足を前に伸ばしてスライディングすると、立ち上がった時体が次の塁の方を向きスタートを切りやすい。

第125回 ノーヒットノーラン発生確率についての誤解

平均的な投手は何試合に1回の割合で達成するか

平均的な能力を持った投手がノーヒットノーランを達成する確率を計算します。

NPB(2019年)では、平均打率＝総安打数/総打数＝14551/57729=.252なので、平均的な投手の被打率を切りよくR1＝.250とします。

ヒットを打たれずアウトにする確率は1-R1で、それをx乗したものがx人連続でアウトする確率になります。

1人目をアウトにする確率は1-R1=.750です。

3人連続でアウトにする確率は(1-R1)^3=0.422です。

27人連続でアウトにする確率は(1-R1)^27=0.00042です。

平均的な投手がノーノーを達成する確率は0.042%です。

これは3人連続でアウトにする確率の1/1000なので、ノーノー達成は三者凡退の1000も倍難しいということになります。

何試合に1回の割合でノーノーが発生するかは、発生確率の逆数で求められます。

N=1/(1-R1)^27=2362試合

被打率.250の平均的な投手は2362試合に1回の割合でノーノーを達成します。

2362試合投げたら

では、この投手が2362試合に先発登板したら必ず、100%ノーノー達成できるかといえば、そうではありませんね。

一等当選確率が一千万分の一のジャンボ宝くじを一千万枚買っても、一等が当たらないことがあるのと同じです。

2362試合に1度の割合でノーノー達成する投手が、2362試合に投げた時1回以上ノーノー達成している確率はどれくらいだと思いますか？

（一人の投手が現役中に2362試合先発登板するのは現実的でないので、同じ被打率の投手たちが延べ2362試合に投げるとして考えてください。）

90%？95%? 

100%でないにしても、それに近い高確率だとイメージしているのではないでしょうか。

実はもっとずっと低いのです。

登板数を重ねるごとに1回以上ノーノー達成している確率がどうなるか、計算します。

先ほどのノーノー達成率をR2とすると、ノーノーがx試合連続で達成されない確率は(1-R2)^xなので、x試合登板で1回以上ノーノー達成する確率は1-(1-R2)^xとなります。

1試合登板でノーノー達成確率はR2=0.00042です。

2試合登板でノーノー達成確率は1-(1-R2)^2=0.00085です。

200試合登板でノーノー達成確率は1-(1-R2)^200=0.081です。

2362試合登板でノーノー達成確率は1-(1-R2)^2362=0.632です。

2362試合登板したとき1度はノーノー達成している確率は63.2%です。2/3弱であり、100%よりもずっと小さい確率です。

優秀な投手は何試合に1回の割合で達成するか

今度は、優秀な投手の場合でノーノー達成率を計算します。

被打率R1=.200とします。

2021年のNPBで被打率.200以下はオリックス山本投手(.182、100投球回以上)ただ一人ですから、被打率.200なら沢村賞レベルのとても優秀な投手を想定していることになります。

1人目をアウトにする確率は1-R1=.800です。

3人連続でアウトにする確率は(1-R1)^3=0.512です。

27人連続でアウトにする確率は(1-R1)^27=0.00242です。

優秀な投手がノーノーを達成する確率は0.242%です。

平均的な投手(0.042%)の5倍以上の確率です。

続いて、何試合に1回の割合でノーノーが発生するかを計算します。

N=1/(1-R1)^27=414試合

被打率.200の優秀な投手は414試合に1回の割合でノーノーを達成します。

414試合先発登板もかなり高いハードルですが、毎年25試合登板し続けると17年目に到達できます。

最後に、この投手が414試合登板したとき1回以上ノーノー達成している確率を計算します。

1試合登板でノーノー達成確率はR2=0.00242です。

414試合登板でノーノー達成確率は1-(1-R2)^414=0.633です。

414試合登板に1回の割合でノーノー発生する投手が、414試合に登板したとき1度はノーノー達成している確率は63.3%です。

やはり100%からは程遠い値です。

先の平均的な投手の場合とほぼ同じ値ですが、これはたまたではありません。数学的になるべくしてこの値になっているのです。

ネイピア数（もしくは自然対数の底）

N試合に1回の割合で発生するなら、N試合やれば100%近い確率で発生するものだと思ってしまいますが、それは誤解です。

平均するとN試合に1回発生ですが、N試合で2回以上発生することもあるので、N試合で1回も発生しないこともあります。

その確率はNが十分大きい場合、ネイピア数（もしくは自然対数の底） e=2.71828...(無理数。小数点以下無限に数字が続く)を用いて、1-1/e=0.632....で、63.2%になります。(*1)

(*1)参考文献 : 知識ゼロでも楽しく読める!数学のしくみ　加藤文元監修　西東社　2020年発行

エクセルではセルに「=1-1/EXP(1)」と入力すると、この値を出すことができます。

上記の2つの計算結果もこれに近い値になっています。

N試合に一回の割合でノーヒットノーランを達成する投手が、N試合に登板したとき少なくとも1回はノーノー達成ししている確率は、ネイピア数によって支配されており、63.2%に収束します。

3人に1人はN試合投げてもノーノー達成できません。

偉業を成し遂げるには実力と運の両方が必要です。

それでは、また。

第124回 160km/hの"熱量"

 

1.6%の回転

動いているボールは運動エネルギーを持っています。

160km/hの球で計算すると、

E1 = 1/2・m・v^2 = 1/2×0.145×(160/3.6)^2 = 143.5 [J]

(m:ボール重量、v:球速） 

143.5J（ジュール）です。

これは重心の並進運動エネルギーです。

ボールが回転していれば、重心回りの回転運動エネルギーも加わります。

一分間に2300回転の球で計算すると、

 E2 = 1/2・I・ω^2 = 1/2・(2/5・m・(d/2)^2) ・(2π・N/60)^2

      = 1/2× { 2/5×0.145×(0.074/2)^2} × (2×3.14×2300/60)^2 = 2.3[J]

(I:慣性モーメント（一様密度の球を仮定）、d:ボール直径、N:回転数） 

 2.3Jです。

並進よりもずっと小さい値です。

トータルで145.8J(=143.5+2.3)で、回転エネルギーそのうちの1.6%にすぎません。(2.3/145.8=0.016)

回転エネルギーが小さいのは回転中心近くは速度が遅く、また一番速い外表面でも32km/hにすぎないためです。(d/2×ω= 0.074/2×(2π×2300/60)×3.6=32)

ジュールとカロリー

J（ジュール）は、SI単位系におけるエネルギー単位です。

定義は「1ニュートンの力でその方向に 1メートル動かすときの仕事」です。

日常生活においてはあまり使われません。

カロリーのほうがなじみがあります。

私たち人間が、食物から摂取したり、運動で消費するエネルギーは主にkcal(キロカロリー）で表されます。

1カロリーは「水 1gの温度を1 °C上昇させる熱量」で、1キロカロリーはこの1000倍です。

ジュールとカロリーの関係は「1 cal = 4.184 J 」です。

160km/hの熱量

160km/hのボールが持つ運動エネルギーがすべて水の熱量に変換されたら、どのくらい温度が上がるでしょうか。

160km/hのエネルギーは上述のように146Jで、これは35calの熱量と等価です。（146/4.184=35)

200ccの水ならば、わずかに0.2度温度が上昇します。（35/200＝0.17)

観客は沸いてもカップのお湯は沸きません。

ナイアガラの熱量

滝の水は高いところから落ちて力学的な位置エネルギーを熱エネルギーに変換しますが、水温の上昇はわずかです。

ナイアガラの滝でさえ、およそ0.2℃水を温めるだけです。(*1)

160km/hを捕球したキャッチャーミットが高温になり、捕手がやけどすることはありません。

(*1)創元ヴィジュアル科学シリーズ2 シュレディンガーの猫　-実験でたどる物理学の歴史　

      アダム・ハート＝ディヴィス著 山崎正浩訳　創元社　2017年出版

消費カロリー

投手がボールを1球投げるごとに、どのくらいのエネルギーが消費されているでしょうか。

投球の運動強度を6METsとし、体重100kgの投手が、3時間の試合の半分1.5時間で、100球を投げると仮定します。

そのとき1球投げるごとに投手が消費するカロリーは、9.5kcalとなります。(6×100×1.5×1.05/100=9.45)

ここで、

METs　×　体重（kg）　×　時間　×　1.05　＝　消費カロリー（kcal）

です。

160km/hのボールが持つ運動エネルギーは上述のように、35calです。

したがって、投手が消費したカロリーのうち、たったの0.4%がボールの運動エネルギーに変換されています。(35/1000/9.5=0.0037)

とても非効率です。SDGs過激派には知られたくない事実です。

それでは、また。