2つの相対論
大雑把に言うと特殊相対性理論は、光速に近い速度で移動する物体は①進行方向に縮み、②時間の進みが遅くなり、③質量が増加するというものです。
実世界の現象でありながら、日常生活における常識が覆される面白さがあります。
一般相対性理論は、特殊相対性理論を発展させたもので、重力を取り扱います。
720万分の1
光の速度は、秒速30万キロメートルです。
それに対し野球の投球は150km/hほどで、これは秒速42メートルです。
これは光速の1/7200000(=42/300000000)です。7桁小さいオーダーです。
つまり、野球の話をするとき相対性理論の適用は不要です。
つまり、野球の話をするとき相対性理論の適用は不要です。
不要ですが、面白そうなので、今回は野球ボールに相対性理論を適用するとどうなるのか、計算をしてみます。
野球ボールのローレンツ収縮の計算
相対性理論に従えば光速cに近い速度で移動している物体は、静止している人(静止系)から見て移動方向の長さが縮んでいるように見えます。
野球の投球ならホーム-センター方向にボールがつぶれて縦長の楕円形に見えるということが起こります。
空気抵抗などの"力"を受けて変形しているのではなく、"時空"が縮むことにより時空の中に存在するボールも一緒に縮みます。
ローレンツは物理学者の名前です。
相対性理論といえばアインシュタインですが彼の完全な独力でつくり上げられたものではなく、先人達の仕事から多くのヒントを得ています。ローレンツの他にも、ポアンカレ、マッハ、マクスウェル、マイケルソンとモーレーなどが大きな影響を与えています。
それでは、どれくらい縮むのか(縮まないのか)計算してみます。
次は、時間の遅れです。
この虫がどれだけの未来へ時間旅行するのか計算してみます。
時間の遅れの計算式は上図②式のようで、先ほどのローレンツ収縮と同じ形をしています。
これも桁が小さすぎて良く分かりません。

これもやはり桁が小さすぎ、良く分かりません。
ローレンツ収縮の計算式は①式のようです。
この式は三平方の定理から導かれ、誰でも計算できる形をしています。
興味を持って訪れた人にいきなり難解な数式をぶつけて門前払いしてしまわないのも、相対性理論の良いところです。
物体の速度vが光速cよりもずっと小さいときv/c≒0なので、①式のルートの部分がほぼ1となり、L≒Loとなり、ローレンツ収縮の効果がなくなります。
そのため物体の速度vが光速cに比べずっと小さいとき、相対性理論の適用は不要となります。
それでは、どれくらい縮むのか(縮まないのか)計算してみます。
[計算結果]
球速vはメジャーリーグの4シームを想定し、150km/hとします。
①式の計算結果は以下のようです。
他のものと比べると、7×10^-13mmは、電子(古典電子半径 2.8×10^-15m)の大きさの1/8程度です。
肉眼で見て縮んでいるのが分かるようなレベルではありません。
それでもプランク長さよりは長いため実際にボールは収縮しています。
割合で言うと、元の径の0.99999999999999倍に縮みます。小数点の後ろに9が14個も並びます。パーセントで言うと、99.999999999999%です。お酒やドラマの名前がこんなに長ければ、消費者はうんざりしてしまいます。
野球ボールの時間旅行の計算
映画「猿の惑星」ではラストで(※ネタバレ注意)主人公が未来の地球へタイムトラベルしていたことが明らかになります。
相対性理論では光速に近い速度で移動しているものは時間の流れがゆっくりになるため、宇宙船が地球に対して光速近くまで加速していたとすればあり得る話となります。
野球ボールでも、例えば小さな虫がボールに貼り付たまま投げれば、虫は時間旅行をします。キャッチャーミットで受け止められた時までの時間進みの遅さの分だけ、虫にとってグラウンド上の人達は早く時間が進んでいるので、未来の世界に到着することになります。
この虫がどれだけの未来へ時間旅行するのか計算してみます。
時間の遅れの計算式は上図②式のようで、先ほどのローレンツ収縮と同じ形をしています。
[計算結果]
球速vは先ほどと同様に150km/hとします。投げてから捕るまでの飛行時間は0.45秒とし、加速と減速にかかる時間は無視します。
②式の計算結果は、以下のようです。
球速150km/hの球に貼り付いた虫は、4×10^-15秒だけ未来へ時間旅行をします。
光は1秒間に地球7周半分の距離を進みますが、4×10^-15秒の間ではわずか千分の一ミリしか進めません。それだけの短い時間です。
それでもプランク時間よりは長い時間のため実際に時間旅行は起こっています。
10^-15秒の時間遅れでは、例え何万、何億球投げようとも、この虫が22世紀まで長生きすることはできそうもありません。
それどころかむしろ空気中で音速を超えるときの衝撃波や、摩擦による熱のダメージで寿命を縮めてしまうことでしょう。
またボールの時間遅れはこのように極めて小さいため、速球王の中に仕込まれたストップウォッチを相対論に基づいて補正する必要はありません。
野球ボールの質量増加の計算
最後は質量の増加です。
「質量はエネルギーと等価」というフレーズおよび「E=mc^2」の式は、相対性理論の中でも最も有名な部分の一つです。
アインシュタインを尊敬する人は彼のおかげで原子力発電ができたと称え、そうでない人は彼のせいで核兵器が生まれたと非難します。世界が平和になりますように。
投手の投げた野球ボールは運動エネルギーの分だけ静止時より多くのエネルギーを持っており、その分だけ質量mが増加します。
質量増加の計算式は上図③のようです。これもまたローレンツ収縮と同じ形の式をしていますが、質量は増える方向なのでルートの部分で割る形になります。
では、どれくらい質量が増加しているのか計算してみます。
[計算結果]
球速vは先と同様に150km/hとします。ボールの静止質量は0.145kgとします。
③式の計算結果は以下のようです。

球速150km/hの投球は、質量が1×10^-15kg増加します。
他のものと比べると、人の細胞一個の中にあるDNA(3×10^-15kg)の1/3程度です。
割合で言うと元の質量の1.00000000000001倍、100兆分の1倍だけ増加します。
これだけわずかなので投手がリリースの瞬間に「ボールが重くなった」と感じることはありません。
もしそう感じたとしてもそれは相対性理論の効果による質量増加ではなく、加速時の慣性力です。ボールを押した分だけ手が押し返される「反作用」の力です。

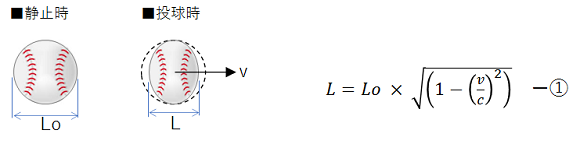







0 件のコメント:
コメントを投稿