第128回 150km/hの縫い目の軌跡

 

投手の投げたボールは回転しながらキャッチャーミットに向かって飛んでいきます。

ボールの重心は並進運動をし、ボール表面上の点は重心回りに円運動をします。

この2つが組み合わさった縫い目はどのような軌跡を描くでしょうか？

計算してみます。

縫い目の位置の計算式

ボールが速度vでx方向に飛んでいくとき、重心位置は下式のようになります。

ボール重心の位置

xo = vt ,  zo=0 

(t: 経過時間）

ここで、t=0での重心位置を原点とし、x-z平面上で動くとします。xが投球方向,zが上空方向です。

今回はリリース直後のみを想定し、重力と空気力の影響は無視します。

ボールが回転数Nでy軸周りに回転する（バックスピン回転）とき、縫い目の位置は下式のようになります。

縫い目の位置

x=r・cos(ωt+θ)+xo , z=r・sin(ωt+θ)

ここで、ω=2πN

(r:ボール半径、ω:角速度、t: 経過時間、θ：初期角度）

縫い目の軌跡計算

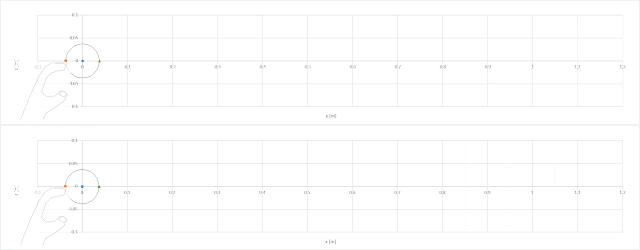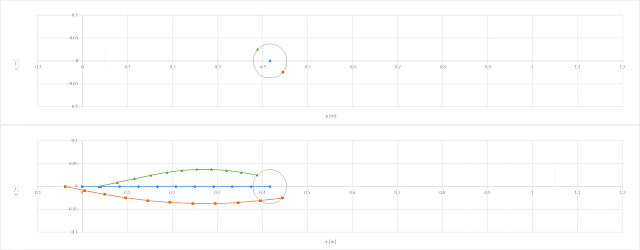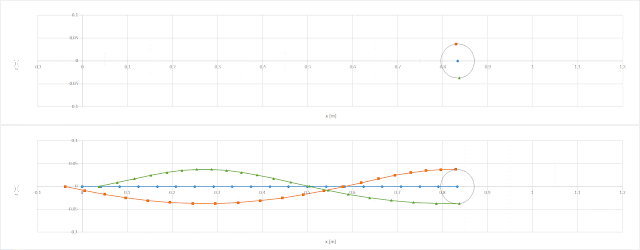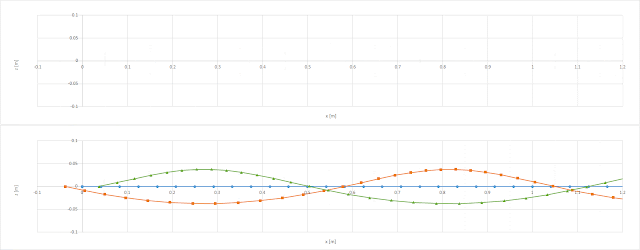
球速v=150km/h、回転数N=2300rpmとして上式で重心および縫い目2か所の軌跡を計算した結果が、以下です。

gif動画

1/100倍スローです。

静止画

グラフ上の点は0.001秒ごとの位置を表します。点と点の間隔の広いほど速い速度で動いています。

縫い目が上側来たときは間隔が狭く、下側では広くなっています。

上図で左回りのバックスピン回転により、上側では後ろに戻る方向に動き、速度が遅くなります。下側は前に進む方向なので速くなります。

縫い目は重心に対し32.5km/hで回転しているため、上側は117.5km/h(=150-32.5)、下側は182.5km/h(=150+32.5)でそれぞれ動いています。

上下の差は65km/h(=32.5×2)にもなります。

この上下の速度差が空気の圧力差を生み出し、それがボールをホップさせる上向き揚力となります。

*****

球速と回転数、つまり中心点の移動速度と角速度、には関連がないためこの曲線はサイクロイドでもなければ、サインカーブでもありません。

数学上の呼び名は特にありませんが、幾何学的な美しさがあり見ていて心地のよい曲線です。

ではまた。