
ゆっくりに見える1041km/h
上空を飛んでいる飛行機はマッハ0.85という超高速で移動していますが、とてもそうは見えません。まるで空に貼り付いてしまったかのようゆっくりゆっくりと進み、いつまでたっても視界から消えずにいます。飛行機よりも、野球のボールの方がよっぽど速く見えます。
マッハ0.85は時速で言うと、1041km/hです。
マッハ1が音速、つまり空気中を音が伝わる速さです。物理学的に言うと空気が圧縮されて密度の高いところと、反対に密度の低いところが交互にできる「疎密波」が伝搬する速度です。この音速を超えてしまうと空気が極限まで圧縮されたところを機体が突き抜けていくことになり、その時の衝撃波により機体がダメージを受けるため、コストや安全性が重視される民間機ではそれよりも少し小さい速度で飛んでいます。
そんな1000km/hを超える高速で移動している飛行機よりも、打者の目前を通過する140km/hの野球ボールの方がずっと速く見えるは、いったいなぜでしょうか?
目は角度で物を見る
それは、人間の目が、物体の動きを「角度の変化」として捉えているからです。
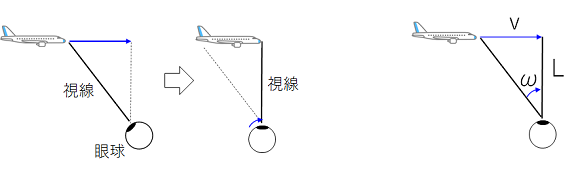
下図のように飛行機が左から右へ動き、それをずっと見続けるとします。
このとき視線を左から右へ移動させるために、眼球は右回りに回転します。
あるいは眼球を動かさずに、顔や体を動かす人もいるかもしれませんが、いずれにしろ視線を移動させるために回転します。
そのため、人間の目は物体の速さを、実際の速度vではなく、視線が回転する速度ωとして認識するのです。
この視線が回転する速度ωは、角度の変化する速さ、言い換えると単位時間に変化する角度の大きさで、物理学では「角速度」と呼びます。
飛行機は高いところを飛んでおり目から物体までの距離Lがとても大きいため、速度vが大きくても、角速度ωは小さくなります。
上の図でいうとすごく縦に細長い、ωの部分の角がとがった三角形になります。
その結果、人間の目にはゆっくりに見えるのです。
飛行機の角速度の計算
では実際、飛行機と野球のボールで角速度ω、つまり人間の目が認識する速さ、はどれくらい異なるのか計算してみます。
[計算式]
角速度は先の図に示されるように、以下の式で計算されます。
tan ω = v / L
(ω:角速度、L:目から物体までの距離、v:物体の速度)
これは三角関数の式と同じ形です。
Lは普通の距離ですが、vが速度、つまり距離を時間微分したものになっているため、左辺のtanも普通の角度θではなく、角度の変化する速さである角度ω(=dθ/dt)になるわけです。
三角関数の性質でv/L<<1のとき、tanω≒ωとなります。
ω = v / L
[計算結果]
距離L
民間機の場合、上空1万メートルあたりを巡航します(L=10000m)。
民間機は燃費を重視します。
高いところを飛ぶほど空気が薄くなり空気抵抗は減るのですが、一方であまり空気が薄くなりすぎるとエンジンで燃料を燃やすための酸素が少なくなってしまいます。
最も燃費がよくなる落としどころを探した結果、この高さを飛ぶことになりました。
速度v
速度vの単位は距離Lと合わせるためm/sを用います。
v= 1041km/h = 289m/s
角速度ω
ω = v / L = 289 / 10000 =0.0289 [rad/s]
ω=0.0289 × (180/3.14) = 1.7 [deg/s]
イメージが湧きやすいよう角度の単位をラジアン(rad)から度(°、deg)に変換しました。
時速1041km/hで上空一万メートルの飛行機を見続ける眼球は、一秒間に1.7度回転するという結果になりました。
一秒間の眼球の回転角度がわずか1.7度なので、本当はすごいスピードで飛んでいるのに、地上にいる人間の目にはゆっくりに見える、というわけです。
野球ボールの角速度の計算
次は野球のボールです。
[計算式]
先ほどと同様に、以下の式で計算されます。
tan ω = v / L
今回はv/L<<1ではないので、tanω≒ωは使えません。
そのため、アークタンジェント(tan^-1)で求めます。
ω = tan^-1 (v / L)
[計算結果]
距離L
ストライクゾーンを通過するボールを打者が見ると想定して、目からボールまでの距離は1メートルとします(L=1m)。
速度v
投球はリリースからホームベースに達するまでに十数キロ減速するので、初速150km/h以上の球でもホームベース上では140km/h程度になります。
v= 140km/h = 39m/s
角速度ω
tan ω = v / L = 39 / 1 =39
ω=tan^-1ω = 1.55 [rad/s]
ω=1.55 × (180/3.14) = 88.5 [deg/s]
アークタンジェント(tan^-1)は自力で計算するのは大変ですが、エクセルや関数電卓を使うと簡単に求められます。
こちらもイメージが湧きやすいよう角度の単位をラジアン(rad)から度(°、deg)に変換しました。
時速140km/hで目の前一メートルを横切る野球ボールを見続ける眼球は、一秒間に88.5度回転しなければならない、という結果になりました。
飛行機と比べると53倍(=88.5/1.7)の速さで回転させることになります。
そのため飛行機よりもずっと速く見えるわけです。
打者はボールをそれほど見ていない
上記のように野球ボールを見続けるためには、一秒間に眼球をほぼ90度回転させなければいけないのですが、そんなに速く眼球を動かすことはできるのか。
というと、できないようです。
そのため打者は、こんなボールの見方をしているようです。
●リリース直後
まず打者はボールを視界の真ん中でピントを合わせてみることをせず、周辺視野で捉えています。
リリース前もボールではなく、肘の当たりをぼんやり見ています。
宮本武蔵が五輪の書において推奨している、「見の目弱く、観の目強く」は剣術に限らず野球のバッティングでも有効なわけです。
周辺視野は、解像度が低いためボールに書かれた文字を読んだり、ひげの一本多いドラえもんの絵が描かれているのをしっかり見たりすることはできませんが、物体の動きを捉えるのは視野の中心部よりも得意です。
●ホームベース数メートル手前
次に打者は投球軌道を予測し、ボールが飛んでくるはずのところにあらかじめ視線を先回りさせておきます。
ずっと追いかけ続けることはできないから、待ち伏せをするわけです。
そして予測通りの位置にボールが来れば、バッチリとピントが合って、まるで「ボールが止まって見えた」ように感じます。
逆に予想以上の変化をすると、待ち伏せした場所と全然違う所をボールが通過していくため、見失ってしまい、まるで「ボールが消えた」ように感じます。
●ホームベース上
そして最後、ボールとバットが衝突する瞬間、打者はボールを見ていません。
自分が振ろうとしているところと、ボールが飛んでくるところがずれていることに気づいたら、バットの軌道を修正しようとします。
しかし、人間が目で見て、脳で判断して、筋肉に指令を出して、筋繊維が縮んで体が動いて、バットの動きに反映されるという一連のことが行われるまでに、どうやっても0.1秒以上の時間がかかります。
そのため、インパクトまで0.1秒を切ったタイミングではもう、ボールを見ても見なくても打撃結果は変わらないのです。
見ても意味がないから、見てないのです。
またバットに当たるところまでボールを見ようとすると、頭は体と反対方向に回転します。
右打者の場合、真上から見て体は左回りに回転しますが、ボールを最後まで見ようとする人の頭部は右回りに回転します。
人間の頭部は6-7kgほどと、意外と重量があるため、体と反対に回転するとスイングの威力を鈍らせてしまいます。
見ない方がいいから見ないのです。
投手の中には、中日の大野投手のように首を横に振って投げる人もいますが、これは逆に頭部の回転により体の回転を加速させているのです。
実際ボールがバットに当たる瞬間をとらえた写真をみると、大半の打者の視線はボールよりも2メートルぐらい前方を向いています。中には、目をつぶっている人もいて面白いです。
まとめ
今回の計算結果のまとめです。
- 人間の目は物体の速さを実際の速度vではなく、視線が回転する速度ωとして認識する
- 上空の飛行機を見続ける眼球は、一秒間に1.7度しか回転しないので、ゆっくりに見える
- 目の前のボールを見続ける眼球は、一秒間に88.5も回転しなければならないので、速く見える。
- 人間の目ではボールを見続けることができないため、打者はそれほどよく見ずに打っている。
*****
少年野球のコーチからプロの解説者まで「ボールは最後まで良く見ろ」といいます。
実際には最後の最後は見ていないわけですが、わざと嘘をついているとは思えません。
頭の中の認識では最後まで見ているつもりなのですが、球が速すぎて人間の目ではとらえきれないものをそれでも何とかして打ち返そうとした結果、無意識で見ないようにしているため認識と実際の動きに齟齬が出るのです。
野球をやっている人なら、サヨナラヒットや大事な試合でのホームランなど、野球人生の中でも印象深い一打はスローモーションで記憶に焼き付いていると思います。
その記憶を、ゆっくりと反芻してみてください。
投手が投げボールが近づいてきてバットを振る。打ち返した打球が空を飛んでいく。
その間にボールがバットに当たった瞬間の映像が見えますか?
恐らくは見えないでしょう。
(私の場合は、一瞬真っ暗な映像が挟まれます。)






0 件のコメント:
コメントを投稿