第92回 Excelで野球場を作図する

幾何学的

野球のグラウンドはルールにより各寸法が定められており、それは幾何学的に整った形をしています。

そのため、適当な座標系を指定し、簡単な寸法計算をするだけで作図することができます。

そこで今回は野球のグラウンドを、Excelを使って描いてみたいと思います。

ホームベース

まず最初は、ホームベースです。

投球のストライクゾーンおよび、得点を定める肝心かなめの存在です。

家のような形をしているため"ホーム"ベースと呼ばれますが、正五角形ではなく、一辺が43.2cmの正方形の角2つを辺の中点で結ぶラインで切り落とした形をしています。

ベース後端(捕手側)の点を原点にとり、センターラインをy軸、一塁方向を+x軸にとります。

Excelで計算した値と式、および散布図でプロットした結果は以下のようです。単位はメートルです。

バッターボックス、ファールライン

次は左右のバッターボックスとライト、レフトのファールラインです。

打者はバッターボックスの外に完全に足が出た状態でボールを打つと、アウトになります。

ファールラインは長打のヒットとファールを分ける、あるいは絶妙なバントとファールを分け、時に勝負の行方を左右する存在です。

バッターボックスは縦1.824メートル、横1.219メートルの長方形です。前後の中心はホームベースの中点(上図の点1)で、左右のバッタボークスはホームベースを挟んで73.66メートル離れた左右対称な配置になっています。

寸法の値に小数点以下が多い数字になっているのは、野球発祥国であるアメリカで使われている長さの単位フィートでキリの良い値にされているのを、メートルに換算しているためです。

ファールラインはホームベース後端(上図の点0)からセンターラインに対しそれぞれ45度の方向に100メートル先まで伸ばされた直線(線分)です。45度のため、√2で割るだけでの伸ばした先の端点、すなわち両翼ポールの点のx,y座標を求めることができます(cos45°=sin45°=1/√2)。またファールライには通常バッターボックスの前端から線を引かれます。

Excelで計算した値と式、および散布図でプロットした結果は以下のようです。

123塁ベース、ピッチャープレート

次は1,2,3塁の各ベースと、ピッチャープレートです。

1塁ベースはライト線上、ホームベース後端から27.431メートルの位置を後端とする、一辺38.1cmの正方形です。

2塁ベースの中心点はセンターライン上、ホームベース後端から38.795メートルの位置にあります。サイズは一塁と同じです。

3塁ベースは、1塁ベースをセンターラインに対して左右反転させた位置にあります。サイズは1塁と同じです。

ピッチャープレートはホームベース後端から18.44メートルの位置ある、縦15.2cm、横60.9cmの長方形です。

Excelで計算した値と式、および散布図でプロットした結果は以下のようです。

これで、直線で描ける部分は完成です。

けん制球が難しい理由

私は子供の頃からずっと野球をしているのですが、今回作図をしていて初めて気づいたことがあります。

ピッチャープレートは1塁と3塁を結ぶライン上ではなく、少し手前の、ホームベース寄りにあります(y29=18.44 < y21=19.397) 。

けん制球というのはどうも投げづらいものだと常々思っていたのですが、このせいだということが分かりました。案外気が付かないものです。

3塁へのけん制球はセットポジションから体の真正面でなく、1メートル弱右側に向かって投げているわけです。同様に1塁けん制では180度真後ろではなく、もう少し深い角度まで回転して投げなければいけません。

また2塁けん制では、ホームに投げるよりも2メートル弱長い距離を投げる(y29=18.44 < y25-y29 =20.355)ことになります。ホームと同じつもりで投げると届かずワンバウンドを放ってしまいます。

ピッチャーマウンド、インフィールドライン

さて次は、ピッチャーマウンドとインフィールドラインです。これは円と円弧で描かれます。

ピッチャーマウンドは土が盛られているだけで、グランド上に線は描かれません。

またインフィールドラインは、学生野球や草野球のグランウンドでは通常省略され、プロやメジャーリーグの球場でも内野が土の場合は外野の芝生との境目で代用し省略されます。

そのため無くても良いのですが、あったほうが雰囲気が出るので、作図します。

ちなみにインフィールドラインは、審判がインフィールドフライを宣告するか否かの判断をする際の目安として引かれているものです。目安でしかなく、宣告するか否かは審判の個々の判断に任されます。選手や観客には直接関係ありませんが、内野手の守備位置の深さを見る際の目安として利用できます。

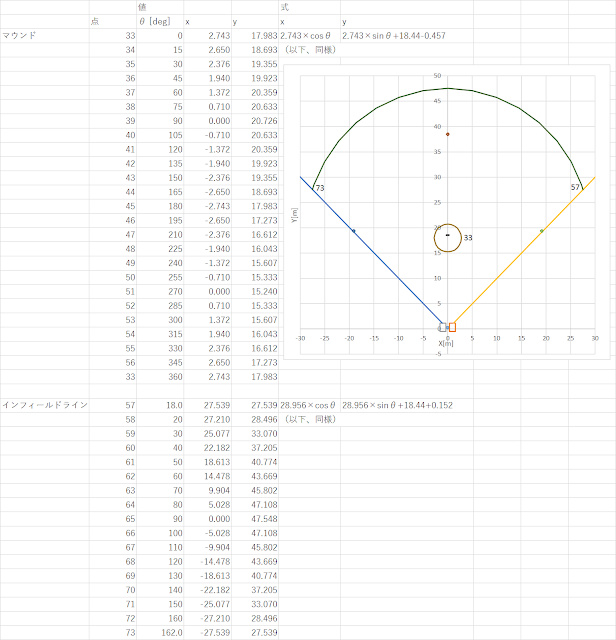
マウンドの中心点はプレート上ではなく、その45.7cm手前にあります。(x,y)=(0,18.44-0.457)を中心とした、半径2.743メートルの円形です。

インフィールドラインはピッチャープレートを中心点とした、半径28.956メートルの円弧です。そのためホームベースからの距離はファールライン際では近く、センターラインよりでは遠くなっています。

点を結んで正確な円や円弧を描こうとすると、無数の点が必要となります。実用的な方法として、等角度おきに点を配置した正多角形で近似します。正多角形で近似する方法は円周率の値を求める際などにも利用されます。

今回はマウンドは15度おきにします。360/15=24なので、正24角形となります。

インフィールドラインは半径が大きいので、プロットした時線がガタガタにならないようもう少し細かくして10度おきにします。

cosとsinでxとyの座標値を計算していくのですが、Excel数式では三角関数を計算する際、角度をなじみのある度(deg)から、ラジアン(rad)に必要があることに注意です。セルへの数式入力の仕方は"RADIANS"を使って、例えば"=2.743*COS(RADIANS(0))"とします(下図のx33の場合)。

Excelで計算した値と式、および散布図でプロットした結果は以下のようです。

いい感じになってきました。

外野フェンス

最後は、外野フェンスです。

ホームランと2ベースヒットを仕分ける存在であり、選手がプレーするグラウンドと観客席を隔てる存在でもあります。

他の寸法と異なり、一定ではなく、球場により形状が異なるのが特徴です。

[バンテリン]

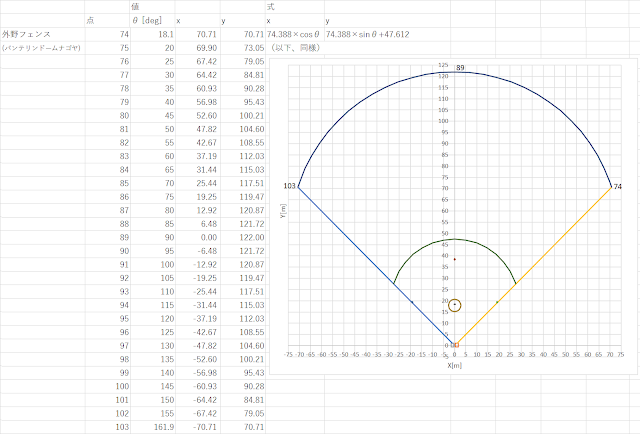
今回は、バンテリンドームナゴヤ(以下、バンテリン)の外野フェンスを作図します。

バンテリンの外野フェンスは他球場よりも右中間、左中間が深くホームランが出にくいのが特徴です。正直、ファンからも不評でホームランテラス待望論が出ていますが、私はこの形が好きです。

なぜかというと、バンテリンの外野フェンスは幾何学的に美しい同心円だからです。円形をしたドーム全体や内外野をぐるっと一周する5階席と同じ中心点で描かれた、円弧になっています。

巨大建築の美しさは古来から幾何学的美しさと切っても切れない関係です。エジプトのピラミッドが何千年も姿を姿を保ちながら多くの考古学者や観光客を魅了しているのも正四角すいの持つ幾何学的な力があるからこそです。

[円弧の中心点]

バンテリンの外野フェンスは円弧ですが、その中心点はどこにあるでしょうか？

外野フェンスは両翼100メートル、センター122メートルです。

一般的な数学の定理として、円弧上の3点の位置が分かれば、その中心点を求めることができます。下図のように3点a,b,cがあれば、aとbをつなぐ直線の垂直二等分線と、bとcをつなぐ直線の垂直二等分線が交わるところ、そこが円弧の中心点です。この方法は、紙の上に作図する際はコンパスと定規で簡単にできるのですが、座標値を計算するのは意外と面倒です。

そこで今回は、外野フェンスが左右対称で点bとOがセンターライン上にある、つまりx座標が0であることを利用して計算します。

中心点Oの座標を(x,y)=(0,yo)とおくと、点bの座標は(0,122)なので、円弧の半径rは

r=122-yo　－①

となります。

また点aの座標は(100/√2,100/√2)なので、円弧の半径rは三平方の定理から

r^2 = (100/√2)^2 + (100/√2 - yo)^2　－②

となります。

①を②に代入してrを消し、yoについて整理すると

yo=(122^2-100^2)/(2×122 - 100×√2) = 47.612 [m]

を得ます。

このyoの値を①式に代入すれば、

r=122-47.612=74.388 [m]

を得ます。

というわけで、バンテリンドームナゴヤの外野フェンスは、ホームベースからセンター方向へ47.612メートルの位置に中心点を持つ、半径74.388メートルの円弧である、ということが分かりました。

[作図]

では、これを基に外野フェンスの座標を5度おきで計算していきます。Excelで計算した値と式、および散布図でプロットした結果は以下のようです。

完成です!

座標計算した103個の点たちを結ぶことで、野球場を描くことができました。

*****

このグランウンドを使って次回以降、打球や送球の計算をしてみたいと思います。

では、また。