第94回 右前打はどのくらい三進しやすいか

1塁から3塁へ

ランナー1塁の場面でライト方向へヒットが出たとき、一気に3塁まで進むという場面が多くあります。

エンドランの時はもちろん、打球が少し深い位置まで飛んだ時や左右にずれたときには、ランナーコーチが手をぐるぐる回し、それを見たランナーは迷わず2塁ベースを蹴り、加速しながら3塁へ向かっていきます。

一方、レフト前ヒットでは2塁でストップするケースのほうが多いです。

なぜでしょうか？

と、問うまでもありません。

グラウンドを見ればわかるように3塁ベースまでの送球距離はライトからの方がレフトからよりも遠くなります。送球距離が長い分だけ、3塁ベースにボールが届くまで長く時間がかかるので、その間にランナーはより多くの距離を進むことができます。

ライトには強肩を

ライトの選手起用方針は野球のレベルにより、反対になります。

小中学生や草野球など、それほどレベルが高くない野球では、守備の苦手な選手をライトに起用します。

右打者の割合が多く、流し打ちの上手な打者も少ないため、ライトに強い打球が飛ぶ頻度が低いためです。また長方形のグラウンドでは一般的に狭い方をライト側にするため、守備範囲も狭くて済みます。

一方、プロ野球やメジャーリーグ、それに近いレベルの野球では、ライトに守備の得意な選手を配置します。とりわけ肩の強い選手を起用します。打球の飛距離が伸び、グラウンドも広いため、送球開始位置はより遠くなり、ライト方向へのヒットで1塁ランナーが一気に3塁へ進みやすくなるため、それを阻止する狙いがあります。

イチローさんのレーザービームも、ライトを守っていたからこそ生まれたビッグプレーです。

そこで、今回はライトから3塁への送球はレフトからに比べ、どれくらい遠く、どれくらい届くのが遅いのか軌道計算をして求めてみます。

送球距離の幾何学計算

ライト、レフトから3塁ベースまでの送球距離は、2次元平面上の2点間距離として幾何学的に求めることができます。

送球開始点のx,y座標値から3塁ベースのx,y座標値をそれぞれ差し引いたものを2乗して、足し合せて、ルートをとれば求められます。三平方の定理です。

[計算条件]

今回は、センターラインに対し左右対称な右前打と左前打を想定します。センターラインとファールラインの中間の方向、センターラインから22.5°の方向に、ホームベースから70メートル離れた位置から送球を開始するとします。

[計算結果]

ライト及びレフトから3塁ベースまでの送球距離の計算結果は、以下のようです。

前々回で作図したグラウンドを使って、結果をプロットしました。

今回の条件では、ライトからの3塁までの送球距離は64.7メートル、レフトからは45.9メートルとなりました。

ライトからの方が18.8メートル(=64.7-45.9)遠くなっています。ライトの選手はバッテリー間距離(18.44メートル）と同じぐらいの距離だけ余分に遠くまで投げなればならないわけです。

送球時間の軌道計算

では次は、この距離の差がボールが届くまでの時間、送球時間の差としてどのくらいになるのかを、軌道シミュレータver3.2で計算してみたいと思います。

[計算条件]

球速140km/h、回転は完全なバックスピン回転で2000rpmで、ノーカット、ノーバウンド送球とします。

計算しやすいように、3塁ベースを原点として、ライトおよびレフトの送球開始点に向かってx軸をとるような座標系で計算します。

軌道シミュレータver.3.2へのインプット値は以下のようです。

[計算結果]

ライト及びレフトから3塁ベースまでの送球軌道および、送球時の計算結果は、以下のようです。

結果のプロットを静止画とgif動画で示しています。gif動画は実際のスピードと同じにしてあります。

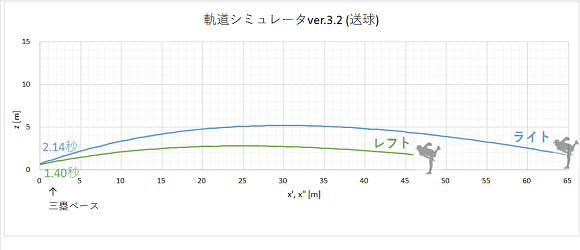
今回の条件では、ライトから3塁まで送球が届くのにかかる時間は2.14秒、レフトからは1.40秒となりました。

ライトからの方が0.74秒(=2.14-1.40)遅くなっています。

投げた瞬間は140km/hの送球も45.9メートル飛んで来る間に空気抵抗でかなり減速します。減速して遅くなった状態で差分の18.8メートルを飛ぶため時間差は大きくなります。

またノーバウンドで投げる場合、距離が長いほど山なり軌道になるため、速度の水平成分が減ります。これによっても少し時間差が広がります。

仮にランナーの走速度が8m/s(=28.8km/h)とすると、この0.74秒の間に5.9メートル(=8×0.74)進むことができます。歩幅を2メートル弱とすると、3歩分ほどです。

というわけで、今回の条件では、右前打で1塁ランナーが3塁へ進むときは、左前打に比べ、送球距離が18.8メートル長くボールが届くのが0.74秒遅れるため、その間にランナーは3歩走って5.9メートル余分に進める、ということが分かりました。

これは、走らないと損ですね。

では、また。