ムーンショット
"Fly to the moon !!! "(月まで飛んでけ!!!)
メジャーリーグの実況では特大ホームランを月まで届くような大飛球という意味で、「ムーンショット」と表現することがあります。
「ムーンショット」の他にも強い打球の比喩として「弾丸ライナー」、「火の出るような当たり」、「ピンポン玉のように飛んでいく」といった表現があります。
どれも一度は聞いたことがあるのではないでしょうか?
もちろん打球は外野席かせいぜい場外駐車場に落ちて、月までは飛んでいかず、ピストルの弾より遅く空中で燃え始めることもありません。
すごさを表現するために、ちょっと大げさに例えることはしばしばあることです。いわゆる"盛る"というやつです。
今回はこれらの例え言葉が実際の打球に比べどのくらい盛られているのか計算してみます。
ムーンショットの盛り率

大谷翔平選手が今日ついに150メートルを超える飛距離を記録しました。
100回の時の計算で超えられるはずだとは思っていたのですが、実際の映像を見るとやはりとんでもない軌道です。
150メートル超えは特大中の特大でメジャーでも数本しか記録されていません。
通常の特大ホームラン、ムーンショットと言われるような打球の飛距離は140メートルほどです。センター方向ならバックスクリーンかさらにはスコアボードを直撃するような大きな当たりです。
一方で、地球から月までの実際の平均距離は38万4400キロメートル(*1)です。
何倍違うか計算すると、
38,440,000/140=2,745,714倍
となります。
6桁も違います。100万倍以上です。
ずいぶんと盛られていますね。メジャーは盛り方もビックです。
アルバトロス
さて。ちょっと寄り道して、ゴルフの話を。

パー5のロングコースを2打でカップインすることを「アルバトロス」と言いますが、これも結構盛っています。
2打で入れるためにはティーショットの飛距離が不可欠ですが、ゴルフのドラコン記録は400ヤード(*2)、メートルで言うと366メートルぐらいです。
アルバトロスは、日本でアホウドリと呼ばれている海鳥のことです。
体に比べて異常に長い翼は翼面積と揚抗比に優れ、普通の海鳥は100kmも飛べば疲れて着陸して休むところ、1000kmをノンストップで渡り切ってしまいます。
盛り率を比べてみると、
1,000,000/366=2,734倍
です。
ゴルフは3桁盛っています。
流体力学的の観点から言えば、球形状が翼型にかなうはずがありません。
弾丸ライナーの盛り率

メジャーリーグで記録された打球速度で最も速いものは190km/h台です。
一方ピストルの弾は、日本警察で採用されているP2000という拳銃で砲口初速は秒速350メートル(*3)です。
ほぼ音速と同じで、時速に直すと1260km/hになります。
比べてみると、
1,260/190=6.6 倍
となります。
ムーンショットに比べると控え目な表現です。日本人はつつましいですね。
銃身の長いライフル銃では力積になる加速距離が長いためもっと砲口初速は大きくなりますが、せいぜい1桁しか違いません。
火の出るような当たりの盛り率
超高速で飛ぶ物体は空中で発火します。
マンガでよく使われる表現なので、聞いた人もイメージしやすいのではないでしょうか。
私はずっと勘違いしていたのですが、これは空気との摩擦熱が原因ではなく、物体前方で圧縮された空気の温度が上昇するために起こるそうです(*4)。
エアコンの暖房と同じ仕組みです。
空気中で発火する速度というのは明確ではないため実際に発火現象を起こしている、隕石の速度を使用します。隕石の速度は秒速18キロメートル(*5)で、これは64,800km/hです。
打球の速度は先と同じく190km/hとして比べてみると、
64800/190=341 倍
となります。
2桁盛っています。
盛り比べ
上記三つの例え言葉の盛り率を比べると、以下のようです。
ムーンショットの盛りすぎが目に余ります。
第二宇宙速度
少し擁護(?)するために、ムーンショットも同じ速度の土俵で比べてみます。
実際にロケットで月まで飛んでいくためには、地球の重力を振り切る必要があります。
これに必要な速度には「第二宇宙速度」というおしゃれな名前がついており、40300km/h(*6)です。
これと190km/hの打球を比べると、ムーンショットの盛り率は
40,300/190=212倍となります。
火の出るような当たりと同レベルに収まりました。(だからなんだという話ですが。)
ピンポン玉のように飛んでいく
さて、最後は「ピンポン玉のように飛んでいく」です。
この表現は多くの野球ファンから突っ込まれたせいか、最近の若いアナウンサーはほとんど言わなくなりました。
ピンポン玉で野球をやって遊んだことのある人は経験あると思いますが、減速が大きくて全然飛びません。
ピンポン玉は軽いので少しの空気抵抗でも大きく減速されてしまいます。
D=m×a
(ここで、D:抗力(空気抵抗)、m:ピンポン玉重量(慣性質量)、a:ピンポン玉の加速度(減速度))
野球ボールに比べ直径が小さいため抗力Dは小さいのですが、それ以上に重量mが小さく慣性が小さいので、加速度aが大きくなりすぐ減速にしてしまいます。
ピンポン玉のように飛んでいくの軌道計算
ピンポン玉を野球のホームランと同じ条件で飛ばしたら、どれくらい飛ぶでしょうか?
軌道計算で求めてみます。
[計算条件]
球速150km/h、バックスピン回転で回転数2700rpm、上向き30度で飛び出すとします。
ピンポン玉は抗力係数CD=0.50,揚力係数CL=0.25(スピンパラメータSP=0.5)(*7)とします。
参考資料(*7)はRe=3.0×10^4のデータで、今回の条件ではRe=1.1×10^5ですがRe=10^3~10^5の範囲ではCD,CLはReの値に依らずほほ横ばいになることが知られているため本計算では同じ値を使用しました。野球はCD=0.41,CL=0.21(SP=0.23)とします。
[計算結果]
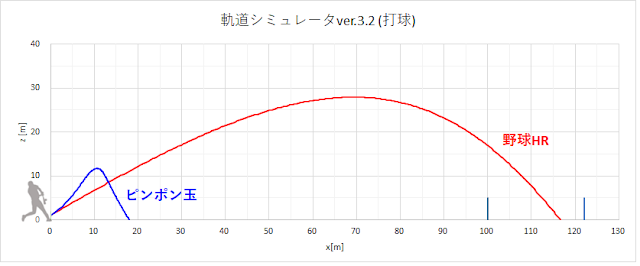
計算結果は以下のようです。
野球の飛距離117メートルに対して、ピンポン玉は18メートルしか飛びません。ピッチャーフライです。
軽くて慣性も重力も小さいので、前半の軌道はバックスピン回転によるマグナス力によって大きく上へ曲がり浮き上がります。後半落ちてくるときは+x方向にもマグナス力が働くため、野球のように上凸ではなく、わずかに下凸の軌道となります。野球では見られない変な軌道です。
というわけで「ピンポン玉のように飛んでいく」は盛っておらず、むしろ控え目な表現です。
マイク・トラウトを捕まえて「アメリカの稲村亜美」と表現するようなものでしょうか。
ちなみに子供のころやったことがあるのですが、ピンポン玉を野球のバットで思い切り打つと、割れます。
ではまた。
参考Webサイト
(*1) Wikipedia
https://ja.wikipedia.org/wiki/%E6%9C%88%E3%81%AE%E8%BB%8C%E9%81%93
(*2)ゴルフダイジェスト社
https://www.golfdigest.co.jp/digest/event/longdrive/past/
(*3) Wikipedia
https://ja.wikipedia.org/wiki/H%26K_P2000
(*4)JAXA
https://iss.jaxa.jp/kids/faq/kidsfaq10.html
(*5)千葉工業大学
http://www.perc.it-chiba.ac.jp/kiji/20130220-RussiaMeteor-wada/Russian_meteorite_FAQ_20130220.htm
(*6)wikipedia
https://ja.wikipedia.org/wiki/%E5%AE%87%E5%AE%99%E9%80%9F%E5%BA%A6
(*7)並列計算技術の数値流体力学への応用
https://i.riken.jp/download/Q18260.pdf#:~:text=%E3%82%B5%E3%83%83%E3%82%AB%E3%83%BC%E3%82%84%E5%8D%93%E7%90%83%E3%81%A8,%E3%81%95%E3%82%8C%E5%A7%8B%E3%82%81%E3%81%A6%E3%81%84%E3%82%8B%EF%BC%8E







0 件のコメント:
コメントを投稿