第110回 低目の球は位置エネルギーにより加速しているか？

高低差

ボールを肩の高さまで持ち上げそっと手を離すと、落ちていきます。

このとき重力により加速され、はじめは止まっていたボールが足元では結構速くなります。物理学ではこの現象を、位置エネルギーがボールの運動エネルギーに変換されたと解釈します。ボールはエネルギーをもらったので動きが速くなります。

これは水平に飛んでいる投球でも同じです。リリースポイントとホームベース上における高低差の分だけ位置エネルギーが運動エネルギーに変換され、鉛直方向の速度が増加します。

位置エネルギーは保存力のため、途中の経路によりません。軌道が直線的でも山なりでも最初と最後の高低差が同じならボールがもらう位置エネルギーは同じです。

低めの球速い説

この理屈でもって、「低めの球速い説」を唱える人がいます。

低めの球は高めの球よりもリリースポイントとの高低差がより大きく、より多くの位置エネルギーが運動エネルギーに変換されるため、同じ初速なら低めの球の方がホームベース上での終速が速い、というわけです。

実際のところ、低目の球はホームベース上でどれくらい加速しているのでしょうか。計算してみます。

概算

リリースポイントの高さを1.8メートル、低目のストライクゾーンを0.5メートルとすれば、高低差は1.3メートルです。

この1.3メートル分の位置エネルギーでどれくらい加速するのか、まずは概算してみます。これは高校物理の計算式で事足ります。

計算式は以下です。

Ep=mgh : 位置エネルギー (m:ボール重量、g:重力加速度、h:高低差）－①

Ek=1/2*m*vz^2 ：運動エネルギー(m:ボール重量、vz:鉛直方向の球速）－②

EpがEkに変換されるので、①=②から

vz=√2gh ‐③　。

③式に値を代入すると、

vz = √2*9.81*1.3 = 5.05 [m/s]

vz =5.05 * 3.6 = 18.2 [km/h]

です。

1.3メートルの高低差で鉛直方向速度は18km/hアップします。結構加速しています。

ただし、この18km/hアップという結果を持って、「低目の球は速い説」を肯定するのは早計です。

これは鉛直方向の速度であり、投球速度の大部分をしめる水平方向の速度とは90度向きが異なります。

そのため単純に足し合せて130km/hの球が、148km/hにアップするというわけにはいかないのです。

簡潔に垂直として速度ベクトルを合成すると、球速は

v=√vx^2+vz^2 = √ 130^2+18^2 = 131.2 [km/h]

となります。

たったの1.2km/hしか速くなりません。

軌道計算

では、次に軌道シミュレータを使用しより実際の投球に近い状態で計算します。低めと高めの球それぞれのホームベース上における終速を計算し比較します。

[計算条件]

初速150km/h、回転数2200rpm、完全なバックスピン回転とします。

リリースポイント高さは1.8メートルで低目のゾーン高さ0.5メートル、高めのゾーンの高さ1.1メートルを通過していくようリリース角度を調整します。

リリースポイントとホームベース上における高低差は、低目の球が1.3メートル、高めの球が0.7メートルになります。

軌道シミュレータver3.2へのインプット値は以下のようです。

[計算結果]

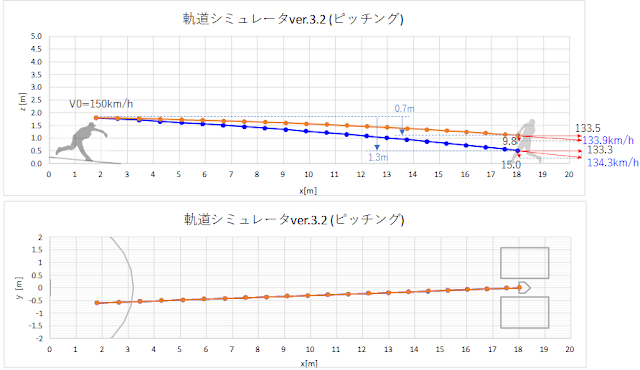
低め、高めの球の軌道計算結果は以下のようです。

グラフ中の点は0.02秒ごとの、一番右端の点のみホームベース前端上(x=18.01m)におけるボール位置を表します。

グラフ上に記載した終速の値は、x=18.01mにおける計算結果値でそれぞれvx=dx/dt、vz=-dz/dt, v=√(dx/dt^2+dy/dt^2+dz/dt^2)です。

低めの球(リリースポイントとの高低差1.3メートル)は、終速度134.3km/hです。高めの球(高低差0.7メートル)は終速133.9km/hです。

初速が同じでも低めの球の方が終速は0.4km/h速い、という結果になりました。

鉛直方向速度vzは低めが15.0km/h、高め9.8はkm/hであり、5km/h以上の差があります。しかしベクトル合成された全体の球速の差は0.4km/hとごくわずかになります。

また、空気抵抗による減速の方が重力による加速よりも大きいため、初速よりも終速の方が遅くなります。

体感速度

0.4km/hの球速差を持って、低めの球の方が速いと結論付けられるでしょうか。打者が感じる体感速度を考えると、そう言い切ることはできません。

リリースからホームベース上に達するまでの時間の計算結果は、低めで0.4133秒、高めで0.4128秒です。低めの球の方が0.0005秒(=0.5ms)遅れをとります。

終速の速い低めの球の方が、ホームベース上に遅れて到達するのです。

この逆転現象が起こる原因は下向きのリリース角度にあります。低めに投げる方がより下向きに投げ出すため、初速の水平方向成分vxが小さくなるためです。

また打者のミートポイントは低目の球では後ろより、高めの球では前よりになります。

この2つの要因の方が、終速がわずかに0.4km/h大きいことの影響を上回り、高めの方が速いと感じるのではないかと考えられます。

また位置エネルギーは保存力で、途中の経路によりません。投球の速度や軌道によらず、誰がどう投げようと、リリースポイントとホームベース上の高低差だけで鉛直方向速度vzの増加量は決まっています。そのため、打者が経験に基づき無意識化で行っているであろう高低差による鉛直速度の加速の予測は、毎回補正いらずで同じように適用することができるゆえに正確であり、その結果位置エネルギーによる鉛直速度の増加により打ちづらさを感じることはないと考えられます。

リリースポイント高いと速い説

「低めの球速い説」と類似で、「リリースポイント高いと速い説」もあります。

リリースポイントの方を高くすることでホームベース上との高低差を大きくし、より多くの位置エネルギーを得るというわけです。

上述の低め高めでは高低差の差が0.6メートル(=1.3-0.7)で、終速の差が0.4km/hでした。

リリースポイントを仮に20cm高くしても、得られる終速アップはこれよりもずっと小さくなります。そのため、リリースポイントを高くすることでの終速アップ効果は実用的なレベルではないということが分かります。

リリースポイントを高くしたことで成績が良くなった投手も大勢いますが、それは終速アップによるものではなく、回転軸や球筋の改善によるものです。

またオーバースローの投手は150km/hなのにアンダーハンドスローでは130km/hしかでないのは位置エネルギーのせいだ、という人もいますが、これはさすがに的外れです。そもそも初速が遅いのですから。

ではまた。