第34回 変化球のときに盗塁するとどのくらいセーフになりやすいのか？

盗塁のセオリー　　　　　　　　　　　　　　　

盗塁するランナーは成功率を高めるために、相手投手が変化球を投げてくるタイミングを狙って走ります。

そのため、以下のようなセオリーがあります。

・足の速いランナーが一塁にいると、バッテリーは盗塁を警戒してストレートを投げる確率が高くなり、その結果打者が狙いを絞りやすくなる。

・ワンボールツーストライクのとき、バッテリーは変化球で三振をとりに来る確率が高いため、盗塁をするチャンスである。

球速の遅い変化球の方が投手がリリースしてからキャッチャーが捕球するまでの時間が長くなります。

その分だけ二塁ベースへ送球が届くのが遅れるため、ランナーが有利、バッテリーは不利になります。

そこで今回は、相手投手が変化球を投げた時に盗塁すると、ストレートの時に比べ、ランナーはどのくらい得するのか計算してみました。

変化球の軌道計算　　　　　　　　　　　　　　　

同じコースに投げられた、プロの標準的なストレート(４シーム)とカーブを計算対象とします。

カーブは、ナックルボールやイーファスピッチのような特殊球を除けば、最も球速が遅い球種です。

キャッチャーの捕球位置はホームベースの後方1m程度と仮定し、プレートから19.5m地点にボールが到達するまでの時間を軌道シミュレーターver.3.2により計算します。

[計算条件]

カーブ
　球速 v0=120[km/h]、リリース角度 θ=3.1度(上向き）
　リリースポイント x0=1.8m(ホーム方向)、y0=-0.5m(三塁方向)、z0=1.8m(高さ）
　ボール回転軸角度 θs=60度、Φs=45度
　回転数 N=2700rpm(SP=0.31) : 抗力係数 CD=0.43、揚力係数CL=0.27

　4シーム
　球速:v0=140[km/h]、リリース角度:θ=-3度(下向き）
　ボール回転軸角度 θs=110度、Φs=-80度
　回転数 N=2200rpm(SP=0.22) : 抗力係数 CD=0.40、揚力係数CL=0.20

　ボール回転軸
　　

  θs : z軸からx-y平面に向かう角度（真上から水平に向かう角度）

  φs : x軸からy軸に向かう角度（ホーム方向から一塁側へ向かう角度）

[計算結果]

同時にリリースし、同じコースに投げられたカーブとストレートの軌道計算結果をプロットすると、以下のようになりました。

上から実際の速度のgif動画、1/10倍スローのgif動画、静止画です。

gif動画（実際の速度）

gif動画（1/10倍スロー）

静止画（点は0.02秒ごとのボール位置を表す。）

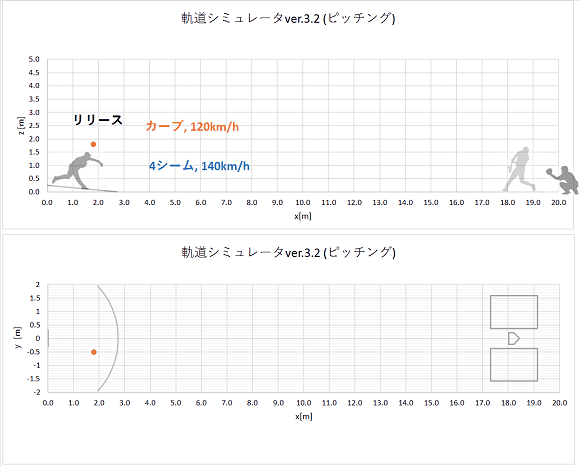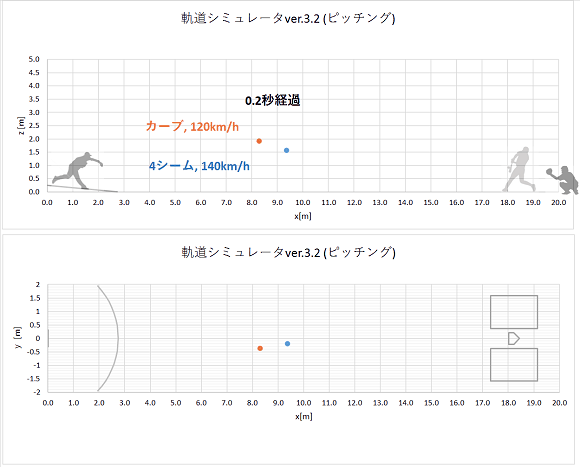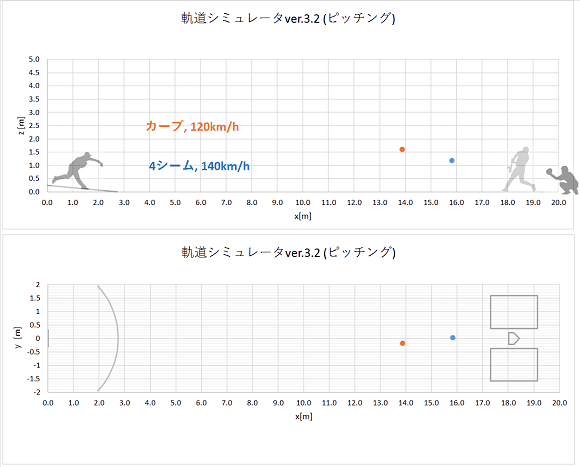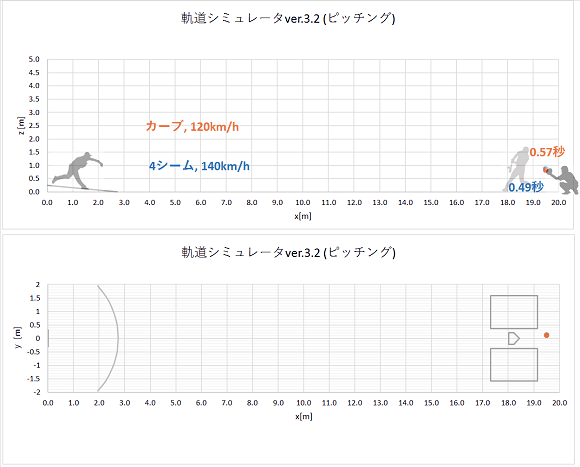
• カーブ(120km/h)はリリースから捕球まで0.57秒かかる
• ストレート(140km/h)はリリースから捕球まで0.49かかる

わずかな時間でも結構進む　　　　　　　　

投手のリリースから捕手の捕球まで、カーブは0.57秒、ストレートは0.49秒かかります。

そのため、カーブの方が0.08秒余計に時間がかかるということになります。

日常生活なら気にも留めないわずかな時間差ですが、盗塁を成功させようと必死に走っているランナーにとっては大きなアドバンテージです。

この0.08秒の間にランナーはどれだけの距離を進めるでしょうか？

ランナーの走速度が時速27km/hとして計算すると、

v=27km/h = 7.5m/s：ランナーの走速度

t=0.08 s　　　　　　：余計に走れる時間

L= v × t  = 7.5 × 0.08 = 0.62 m = 62cm: 余計に走れる距離。

カーブのとき、ランナーはストレート時よりも0.08秒余計に走る時間が与えられ、その間に62センチ余計に距離を走ることができる。

大きなリード　　　　　　　　　　　　　　　

相手投手がカーブを投げる時でもストレートを投げる時でも、ランナーのとるリードの大きさは同じです。

けん制球が来たとき、ぎりぎり戻れるところまでしか出られません。

カーブのとき62センチ余計に走れるということは、言い換えるとストレートのときに62センチより大きくリードをとった状態からスタートできるのと同じです。

そう考えるとカーブのときに盗塁することがいかにランナーにとって有利かが良く分かります。

ランナーを警戒してストレートを投げるか、打者を打ち取るために変化球を投げるか。

バッテリーとの心理的な駆け引きもまた、野球の面白さの一つです。

では、また。

（よかったら押してください。）

　 　
　にほんブログ村