第35回 回転数が多い球は本当にノビるのか？

 

回転数が多いと失速しない？　　　　　

回転数が多いストレートは同じ球速でも威力があり、打たれない。

よくそう言われます。

実際その通りでしょう。

ただし、その説明として「回転数が多いと空気抵抗が小さくなり、失速しないからノビがある」というのは、正しくありません。

なぜなら、抗力係数CDの値は回転数が大きいほど大きくなるからです。

ボールに働く空気抵抗　　　　　

いきなり抗力係数とか言われても知らん、という人もいるでしょうから少し説明します。

まず、ボールは飛んでいる間3つの力「抗力（空気抵抗）」、「揚力」、「重力」を受けます。

●抗力(空気抵抗)D

抗力は進行方向と反対方向にブレーキとして作用する力です。

抗力Dは以下の式で計算されます。

　

（CD:抗力係数、ρ:空気の密度、v:ボールの速度、A:ボールの断面積）

この式中の係数CDが回転数が大きくなると大きくなるため、回転数が大きい方が抗力Dも大きくなります。

つまり回転数が大きい球の方がより大きなブレーキを受けながら飛ぶはずなのです。


●揚力(マグヌス力)L

揚力（マグナス力）は回転により進行方向と垂直方向に曲げる力で、抗力Dと同じ形の式をしています。

この垂直な向き作用する力には、「ボールのスピードは変えずに、向きだけを変える」という特徴があります。

そのため、揚力Lはボールの軌道を曲げるだけで、ブレーキとしては働きません。

揚力Lは以下のような式で表されます。
抗力Dの式の抗力係数CDが揚力係数CLに変わっただけで同じ形をしています。

　

 (CL:揚力係数、ρ:空気の密度、v:ボールの速度、A:ボールの断面積)

　

この式中の係数CLも回転数が大きくなると大きくなるため、回転数が大きい方が揚力Dも大きくなります。

つまり、回転数が大きい球の方がより大きく曲がることになります。

これは経験的な感覚と一致しますね。


●重力
地球がボールを下向きに引き付ける力です。

ボールの回転数によらず一定です。

抗力係数CDとスピンパラメータSP　　　　

抗力係数CD、揚力係数CLは回転数が大きくなるほど大きくなると上述しましたが、正確には回転数と球速の比でによるスピンパラメータSPに依存します。

ここで、

　スピンパラメータ : SP = π×d×N / V。

　（d:ボール直径、N:ボール回転数、V:球速）

スピンパラメータSPの詳細については第2０回を参照ください。

抗力係数CD、揚力係数CLとスピンパラメータSPの関係は、風洞試験や流体解析の結果によるとおおよそ以下のグラフのようになります。

高回転のメリット、デメリット　　　　

実際に値を求めて、比較してみましょう。

●スピンパラメータSP

球速145km/hで高回転数の2500rpmのとき、スピンパラメータは、

 SP = π×d×N / V = 3.14×(7.38/100)×(2500/60) / (145/3.6) = 0.240

となります。

ここで、rpmは一分間当たりの回転数を表す単位です。

上記計算ではSI単位系で計算するため、回転数は一秒間当たりのrpsに、球速は秒速に変換しています。

同様に低回転数の2000rpmについても計算すると、

SP = π×d×N / V = 3.14×(7.38/100)×(2000/60) / (145/3.6) = 0.192

となります。

●抗力係数CD、揚力係数CL

上記のSPをグラフに当てはめることでCD,CLの値を得ます。

2500rpmでは、抗力係数CD=0.41、揚力係数CL=0.22。

2000rpmでは、抗力係数CD=0.40、揚力係数CL=0.18。

これらの値から、同じ球速でも高回転数の2500rpmの方がCDが大きく減速が大きいこと、CLが大きくホップ量が大きいこと、が分かります。

つまり、高回転数のストレートには、減速が大きいというデメリットと、ホップ量が大きいというメリットがあるということです。

高回転と低回転の軌道計算　　　　

では、高回転数による減速とホップ量増加が、実際どのくらいボールの飛び方に違いを生み出しているのか、軌道シミュレーターで軌道計算して検証してみます。

[計算条件]

　4シーム
　球速:v0=145[km/h]、リリース角度:θ=-0.5度(下向き）、φ=2.5度(一塁方向）
　ボール回転軸角度 θs=110度、Φs=-80度
　回転数 N=2500rpm(SP=0.24) : 抗力係数 CD=0.41、揚力係数CL=0.22

     N=2000rpm(SP=0.19) : 抗力係数 CD=0.40、揚力係数CL=0.18

　ボール回転軸
　　

  θs : z軸からx-y平面に向かう角度（真上から水平に向かう角度）

  φs : x軸からy軸に向かう角度（ホーム方向から一塁側へ向かう角度）

[計算結果]

同時にリリースされた、回転数のみ異なるストレートの軌道計算結果をプロットすると、以下のようになりました。

上から実際の速度のgif動画、1/20倍スローのgif動画、静止画です。

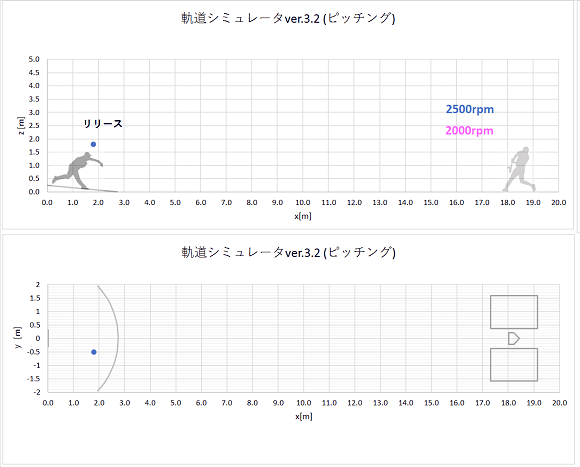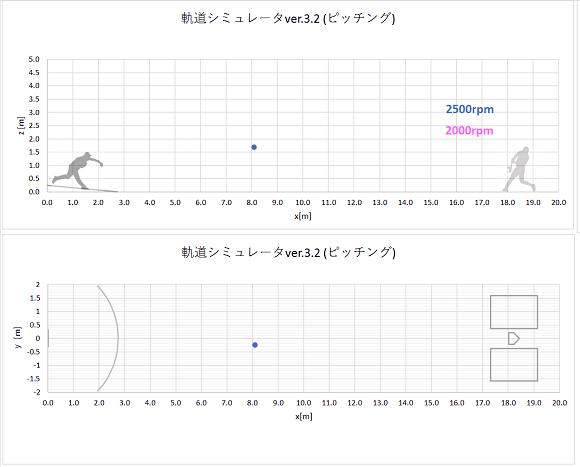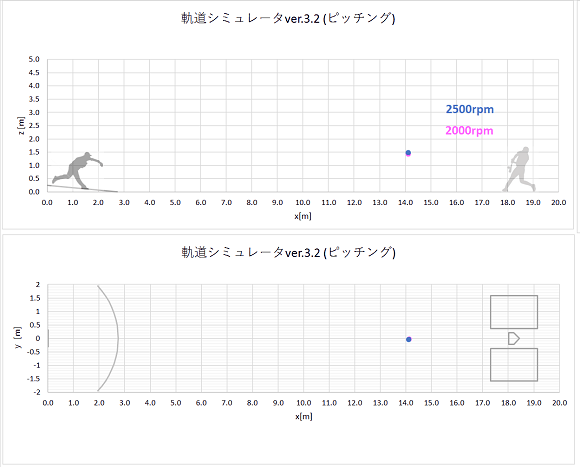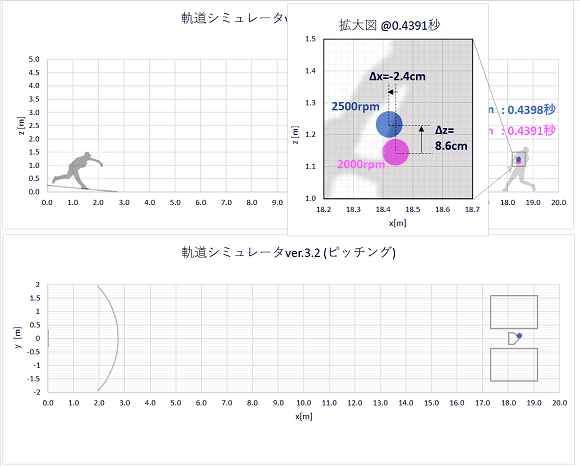
差が小さく分かりづらいのでホームベース到達時の、拡大図も付けました。

gif動画（実際の速度）

gif動画（1/20倍スロー）

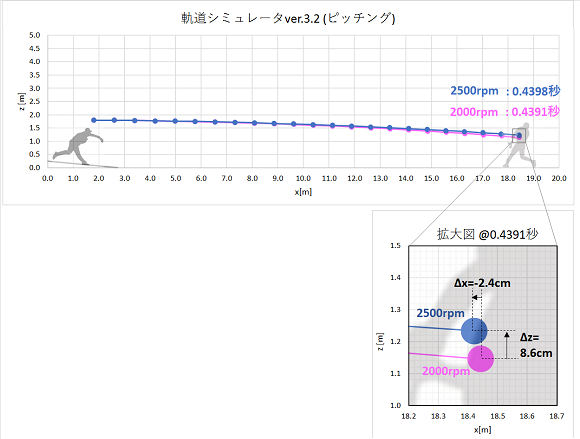
静止画（点は0.02秒ごとのボール位置を表す。）

　2500rpmの高回転は、2000rpmの低回転と比べ、

　・ホームまでの到達時間は、0.0007秒(=0.4398-0.4391)遅れる

　・距離にして2.4cm後れを取る

　・軌道は8.6cm上を通過する。

やはり高回転が優位　　　　

●減速の差

2500rpmの高回転の方が確かに空気抵抗は大きく、ホームまでの到達時間は長くなりますが、その差はわずか0.0007秒です。

これでは人間の感覚として違いを認識することはできないでしょうし、バッターを打ち取るうえでも効果を期待することはできないでしょう。

そのため、回転数による減速の差は、実質的にはない、と言って差し支えないでしょう。

●ホップ量の差

一方で軌道を比べると、2500rpmの高回転の方が8.6cm、ボール一個分以上、上を通過していきます。

そのため、やはり2500rpmの高回転の方がより打ちにくいことは間違いないでしょう。

●打者の感覚

また、打つ時のミートポイントは高めになる程前になります。

そのため、同じタイミングでスイングしても予想より高めにくるほど、差し込まれてしまいます。

これが打者からすると、実際には上下の差を、前後の差、したがって減速の小ささと勘違いさせているのではないか、と推測されます。

●まとめ

・高回転の方が減速は大きい。しかし、ホーム到達時間の差は無視できるほど小さい。

・高回転の方がホップ量が大きくより、高めを通過していく。

・上下のミートポイント位置の違いにより、ホップ量が大きいのを、減速が小さい(ノビがある)と錯覚している可能性がある。

では、また。

（よかったら押してください。）

　 　
　にほんブログ村