第4の力
飛翔中の野球ボールには「重力」、「抗力」、「揚力」の3つの力が働きます。
この前提に基づき軌道シミュレータver3.2は作成されています。
空気中を飛んでいくボールに作用する浮力が、どのくらいの大きさであるか、数字を入れて計算してみましょう。
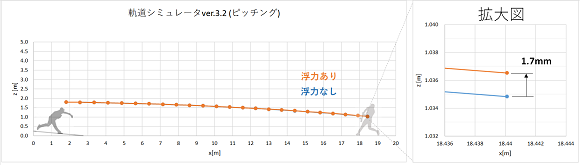
グラフ上の点は0.02秒ごとの、一番右端のみホームベース上(x=18.44m)での、ボール位置を表します。
両者の差がとても小さいので拡大図も追加しました。
やはり省略してもよさそうですね。

私たち人間の体は野球のボールよりも体積が大きいので、その分、浮力も大きくなります。
では、また。
この前提に基づき軌道シミュレータver3.2は作成されています。
しかしながら、厳密に言えばもう一つ、第4の力が作用しています。
それは、「浮力」です。
押しのけた分だけ
浮力とは、流体が物体を上へ押し上げ、浮き上がらせようとする力です。
その大きさは、「物体が押しのけた体積分の流体が受ける重力」と同じになります。
これをアルキメデスの原理といいます。
その大きさは、「物体が押しのけた体積分の流体が受ける重力」と同じになります。
これをアルキメデスの原理といいます。
発見した時、嬉しさのあまり「ヘウレーカ!ヘウレーカ!(見つけた!見つけた!)」と叫びながら裸で走り回った逸話が有名ですね。
アルキメデスの原理
Pf = v×ρ×g : ボールに働く浮力
水は密度が大きいので、浮力が大きく、池に落ちた軟式ボールは沈まずに浮きます。
空気は密度が小さいので、水よりもずっと小さな浮力になります。
飛翔中のボールが受ける浮力
[計算結果]
Pf = v×ρ×g = (2.1×10^-4)×1.205×9.81 =2.49×10^-3[N]
力の単位をN(ニュートン)からなじみのあるキロ、グラムに変換します。
Pf =2.49×10^-3×9.81 = 2.5×10^-4 [kgf]
Pf =2.49×10^-3×9.81 × 1000 = 0.25[gf] : 空気中のボールに働く浮力
ここで、
v=4/3×π×(d/2)^3 = 4/3×π×(0.074)^3
= 2.1×10^-4 [m] : ボールの体積(d:ボールの直径)。
というわけで、空気中のボールに働く浮力は、0.25グラムです。
0.25グラムは1円玉にかかる重力の1/4の大きさです。とても弱い力です。
ボールの重量が145グラムなので、ボールに働く重力の0.17%に過ぎません。
(0.25/145=0.0017)
そのため浮力の影響は無視できると考えて、軌道シミュレータでは考慮しませんでした。
光速よりもはるかに遅い野球ボールに対して相対性理論を考慮しないのと同様です。
浮力を考慮した軌道計算
今回は試みに浮力を考慮した場合と、しない場合でどれくらい投球軌道が変わるのか(変わらないのか)、軌道シミュレータで計算してみます。
無視できると予想されるものでも、一度確認してみることは何事においても大切です。
浮力は重力の0.17%の大きさで、重力と反対方向へ作用するため、軌道シミュレータへインプットする重力定数gを0.9983倍(=1-0.0017)してやります。
そうすることで軌道シミュレータの数式をいじる手間なく、物理的に同じ現象を再現できるからです。
CAEではよく使う手です。
g=9.81[m/s^2] : 重力加速度g'=9.81×0.9983 = 9.79[m/s^2] : 浮力を考慮したインプット値
[計算条件]
以下のような条件で計算します。重力定数g以外は同じです。
プロの平均的4シームを想定しています。
[計算結果]
浮力あり・なしでの投球軌道の計算結果は以下のようになりました。グラフ上の点は0.02秒ごとの、一番右端のみホームベース上(x=18.44m)での、ボール位置を表します。
両者の差がとても小さいので拡大図も追加しました。
やはり省略してもよさそうですね。
余談:体重超過はネリだけでない?

私たち人間の体は野球のボールよりも体積が大きいので、その分、浮力も大きくなります。
大学教授のクリフォード・スワルツさんの概算によれば、体重100kgの人で130gほどの浮力が働き、そのため体重計で測ると本当の体重よりも少し軽め表示されてしまうそうです。
野球選手にとってはどうでもいい話ですが、階級が細かく分かれているせいで厳しい減量を強いられるボクサーにとっては数十グラムの誤差でも大きな問題です。
体重計でリミットぎりぎりだった場合、実際には超過しているかもしれないのです。
自分がリミットよりも200グラム低い体重で計量をパスした後に、相手がぎりぎりでパスだったら、「浮力も考慮しろよ!」と抗議したくなるかもしれませんね。
では、また。






ヤンキースの田中将大はロンドン遠征で、一回を持たず降板しました。ニューヨークとロンドンの緯度の差は10度くらいです。これだけ緯度が違えば微妙に回転軸も回転数も異なるのでは?
返信削除緯度の違いというのは、面白い目の付け所ですね。回転軸や回転数への影響はイメージがつかないですが、地球の自転による遠心力やコリオリの力の影響を計算してみるのもまた楽しいかもしれません。
返信削除