理論から統計の時代へ
例えば、何万球という打球データをホームランになったものとそうでないものに分類し、違いを探せば「打球角度は上向き30度前後で、打球速度は158km/h以上であれば高確率でホームランになる」といったことが分かります。
同じことが理論的な計算によってもできます。
実際、物理学の数式を使った軌道シミュレータver.3.2で計算をしても上記とほぼ同じ結果を得ることができました。(第26回、第28回 参照)
統計的な方法と理論的な方法、それぞれメリットデメリットがあります。
例えば統計的な手法ではこうすればこうなるというインプットとアウトプットの関係は分かるのですが、なぜそうなるのかという理由については分かりません。現象がブラックボックス化されてしまいます。
一方理論的な方法では、計算した結果が本当に現実世界でそうなるのか、計算結果が本当に正しいのかが分かりません。実物での実験や実測と一致することが確認されて初めて信頼されます。
かの有名な一般性相対性理論も数式だけ見て全ての人が納得したわけではなく、重力レンズにより太陽のそばに見える水星の位置がずれるという実現象が確認されたことにより、正しい理論だと認められました。
どれだけ正しそうに見える理論も実現象と合わないのであれば、どこかが間違っているはずです。
上記の第26、28回の記事についても、もし計算結果が統計と一致していなければ私はアップロードせず、計算のミスを探す作業をしていたことでしょう。
逆に言えば統計的手法のメリットは計算と違って間違わないことです。
今までの理論や常識と異なっても、実現象がそうなっているのならばそれが正解です。
理論や常識の方が実現象に合わせて修正され、新しい理論や常識に生まれ変わります。
例えば、地球から見える星の動きを測定し統計的に処理した結果、地動説が生まれ、古い常識の天動説は消え去ったのです。
統計的な方法は実現象だけでなく、計算にも適用できます。
例えば軽さと強度を両立するような航空機の部品を作りたい場合、現在では材料力学の理論に基づいて人間が形状を考えて設計しています。その結果、I型断面の柱などシンプルな形状になります。
しかし今後コンピュータのレベルがますます上がって行けばやがて理論はお構いなしに、何百、何千パターンの形状で次々と強度計算を行い、その中から強度に優れたものを抽出するというように変わってくるでしょう。その結果、人間の骨のような複雑な形状になっていくのではと予想されています。
野球も、野球以外も、時代は理論から統計へと移り変わっていくようです。
変化量のトラッキングデータ
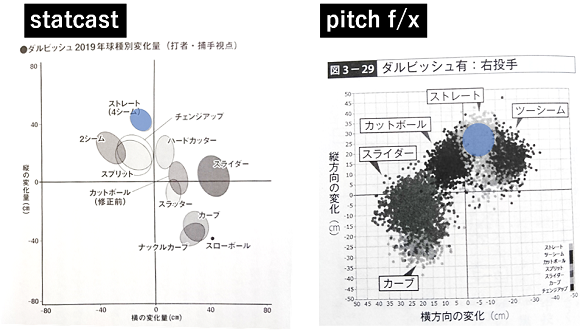
例えばダルビッシュ有投手の場合、下のような散布図で表されるのですが、初めての人は見方が分からず戸惑うようです。
何故かというとこの表は回転により空気から受ける力(マグヌス力)による変化量のみ、言い換えると、重力による自由落下の場合を基準とした変化量を表しているからです。
直線軌道からの変化量をイメージしている、あるいは4シームとの差をイメージしていると全く意味が分からなくなります。
例えば左図の4シームでは40cm強上方向に変化していますが、これは同じ球速、同じリリース角度で投げられた無回転の、ただしナックルボールのような変化はしない球(自由落下)、に比べてホームベース上で40cm強上に到達する、ということを表しています。
直線軌道と比べれば、重力の方がマグナス力よりも強いため、下へ変化した軌道となります。
もし無重力空間で同じ球を投げたのなら本当に直線軌道から40cm強上に曲がる球になります。
また同じ球速の自由落下軌道と比較しているため、実際の投球軌道では140km/hの球の方が100km/hの球よりも重力を受ける時間が短く落下が少ない分、同じ角度でリリースしてもホームベース上でより上の位置に到達しますが、これに関しては一切含まれていません。
あくまで同じ球速の自由落下との相対的な比較です。
なお、横方向の変化は重力の影響を受けないためそのまま直線軌道との差であり、球速が違う球同士でも比べることができます。
科学技術の進歩
上図変化量トラッキングデータは、左は2019年にstatcastで、右は2014年にpitch f/xで測定されたものです。
4シームのホップ量を見ると、左は40cm強に対し、右は25cm程度しかありません。
どうやらpitch f/xの方がstatcastよりもかなり変化量が小さく測定される傾向があったようです。
ダルビッシュ投手に限らず他の投手でも同じ傾向がみられるため、5年の間にMLB投手みんなのホップ量が大幅に増加したと考えるよりは、pitch f/xに測定誤差があったと考える方が自然です。
MLBでは2015年から2017年のあいだにptich f/xからstatcastへ移行されたそうです。
そのためデータを参照するなら2017年以降のものが良いようです。
先ほど、統計は計算と違って結果を間違わないと書きましたが、データの精度が悪ければ間違った答えにたどり着いてしまう危険はあります。
statcastはpitch f/xよりも精度が上がっているはずですが、それでも100%完全ではない部分があることでしょう。
そのため理論や人の感覚の出番はまだあり、同時に科学技術の進歩も待たれます。
ダルビッシュ4シームの軌道計算
トラッキングデータでは変化量に加え、初速と回転数も測定されています。
これら三つのデータから、軌道シミュレータver3.2により投球軌道を計算し再現することができます。
今回はダルビッシュ有投手の4シームについて、トラッキングデータの初速と回転数をインプットとして計算した結果がトラッキングデータの変化量と一致するよう、回転軸の値を調整します。
[トラッキングデータ]
2019年シーズンの平均値です。変化量は先ほどの図左側と同じです。
(引用元:ピッチングデザイン、集英社、お股ニキ著、2020年発行)[計算条件]
軌道シミュレータver3.2へのインプットは以下のようです。
[計算結果]
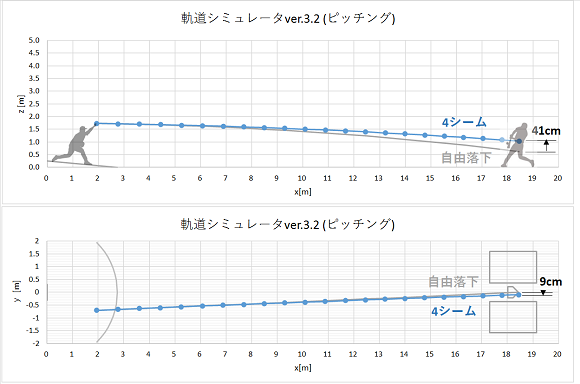
計算された4シームの軌道は以下のようになりました。
図中の点は0.02秒ごとの、一番右はホームベース上(x=18.44m)におけるボール位置です。
灰色線は同じ球速の自由落下軌道で、これとの差が先のトラッキンデータにおける変化量となります。
4シームの特徴
ダルビッシュ投手の4シームの特徴は横方向への変化量が小さいことです。普通の投手の4シームではシュート方向へ20cm前後変化するところ、ダルビッシュ投手は半分以下の9cmのみです。
これは回転軸の横への傾きが小さいということです。普通の投手では20度ほど傾くところ、今回の計算結果ではダルビッシュ投手も回転軸は11度しか横へ傾いていません。(11=101-90)
一般的にこれは良いことです。
回転が傾いていなければそれだけマグナス力のシュート成分が少なく、上向き成分が多くなり、ホップ量が大きくなるからです。
...ところがです。ダルビッシュ投手のホップ量は40cm強であり、これはMLB平均と同程度でしかないのです。
回転軸の横への傾きが小さく、また回転数は平均以上あるのに、ホップ量は平均程度しかないのです。
ジャイロ成分の多い4シーム
それは、回転数や、回転軸の横方向の傾き以外のどこかで、上向き揚力をロスしているということです。
どこか、と考えると、回転軸の真横から前後方向への傾きが大きい、つまりジャイロ成分が大きいということが推測されます。
今回の計算結果によれば、回転軸が32度ほどジャイロ方向へ傾いています。(32=90-58)
これにより変化量は15%減少します。(0.15=1-cos32°=1-0.85)
ダルビッシュ投手のように少し腕が下がったサイドハンド気味の場合、ジャイロ成分をなくそうとするとシュート成分が多くなってしまい、シュート成分をなくそうとするとジャイロ成分が多くなってしまうというジレンマがあります。他の変化球との兼ね合いを考えた結果、後者の回転軸を選んだのではないか、と推測されます。
ジャイロ成分もシュート成分もない完全なバックスピンに近い球を投げるためには、野茂投手やヤクルト小川投手のようにオーバーハンドで真上から投げるフォームでないとむずかしいのです。
逆にサイドハンド気味でジャイロ成分でロスしてしまう分を回転数の多さで補っているとも言うことができます。
ジャイロ成分がなくなれば
今回の計算結果から、もしダルビッシュ投手が「シュート回転しても構わないから、ジャイロ成分がゼロになるような回転軸」で投げれば、変化量はさらに15%アップすることになります。
恐らくですが、それが時折投げる横変化が異常に大きな2シームではないでしょうか。
この球は、お股ツーシームという愛称で呼んでいるそうです。
トラッキングデータ上にある普段投げている2シームは回転数が4シームよりも小さいので、わざと回転数を減らして落としており、これとは別の球種として使い分けていると思われます。
*****
また他の変化球についても次回以降、再現計算をしていきたいと思います。
球種が多すぎて全部できるか、分かりませんが。。
では、また。






0 件のコメント:
コメントを投稿