第40回 ソフトボールの体感速度160キロは本当なのか？

 

5.33メートル手前　　　　

テレビでおなじみの「女子ソフト投手vsプロ野球打者」。

楽しみにして観るのですが、いつも女子ソフトが圧勝します。

プロ野球の打者は振り遅れたかっこ悪い空振りやしょぼい内野ゴロを繰り返し、野球ファンとしては少し悲しくなります。

女子ソフトの速球は110km/hほどで、野球で言えばスローボールに分類される遅さです。

にもかかわらず振り遅れるのは、ソフトボールの方が距離が近いからです。

野球のバッテリー間は18.44メートルですが、女子ソフトボールは13.11メートルで、野球よりも5.33メートルも手前から投げているのです。

さらに野球同様、実際のリリースポイントはプレートよりもだいぶ前であるため、ボールが飛んでくる距離はこれよりも短くなります。

野球よりもずっと近い距離から投げられるため、球速が速くなくても、リリースからホームベースに到達する時間は短くなり、速いと感じるのです。

スイング開始前のボールを見極める時間は同じ球速でも野球よりもずっと短くなり打つのが難しくなります。

テレビなどでは女子ソフトのボールの速球は、野球での160km/hに相当するという意味で、「体感速度160キロ」という表現がされます。

そこで、今回はソフトボールの速球が体感速度として本当に野球の160km/hに相当するのかを、軌道シミュレータver.3.2により計算して求めてみたいと思います。

軌道計算　　　　　

体感速度とは言ったものの、人間の感覚を計算で正確に出すことは容易ではないので、ここでは投手がリリースしてからホームベース上に到達するまでの時間で比較することにします。

[計算条件]
ソフトはライズボールを想定し、バックスピン回転とします。

野球は160km/h、2450rpmのストレートとします。

以下のような条件で計算します。

ボールに関するパラメータもソフトボールに合わせて変更しました。

[計算結果]

時速110km/hのソフトボールの投球と、160km/hの野球の投球の軌道計算結果は以下のようになりました。

両者を重ねてプロットしてみました。

灰色線が野球の、青線がソフトのマウンドとプレートです。ホームベースの位置は合わせてあります。

動画(実際の速度）



動画(1/10倍スロー）



静止画(点は0.02秒ごとのボールの位置を表す)



・野球(160km/h)はリリースからホーム到達まで0.398秒かかる。
・ソフトボール(110km/h)はリリースからホーム到達まで0.404秒かかる。

正確だった　　　　　

野球の160キロは0.398秒、ソフトの110キロは0.404秒。

リリースからホームまでの到達時間はほぼ同じでした。

つまり、「体感速度160キロ」というのは、到達時間を基準とすればかなり正確な表現であることが証明されました。

もしかしたら、最初に体感速度と言い出した人もテレビ局の人も自分の感覚で適当に言ったわけではなく、スロー再生した動画から時間を計測したのかもしれませんね。

ルールごとのチャンピオン　　　　　

格闘技界にはこんな言葉があります。

「世界最強の男なんて存在しない。存在するのはルールごとのチャンピオンだけだ。」

核心をついていると思います。

ボクシングの元ヘビー級王者がキックボクシングの試合に出れば、ローキックを蹴られ続けて何もできなくなる。

キックボクシングの選手が総合の試合に出れば、タックルからのアキレスけん固めで秒殺されるし、ボクシングへの転向に挑戦すれば失敗したりする。

キックと総合の両方で活躍した選手もアマチュアレスリングに復帰すれば二回戦で腕を折られて敗退する。

格闘技転向後は醜態をさらした元横綱の曙も、本職の相撲なら、引退後数年たっていてもボブサップやアリスターオームレイムようなパワーファイターを圧倒できる。

枚挙にいとまがありせん。

レベルが高くなりそれぞれの専門性が高まる程、わずかなルールの違いで強弱が簡単に逆転してしまうのです。

野球でもソフトバンクの周東選手が陸上100mに出場したり、桐生選手が代走で盗塁をしたりしても、きっと大した結果は残せないでしょう。

女子に負けても　　　　　

バッティングも同じです。

ソフトボールと野球は似て非なるスポーツです。

ホーム到達時間が野球の160キロと同じほどの短時間であることに加え、見慣れないウインドミルのフォームと下から投げ上げてくる軌道。

ソフトボールと野球で打者のフォームを見比べるとタイミングをとるための、足の動きがかなり違います。

バットやボールも野球とは異なります。

はたから見ればわずかな違いでも、プレイヤーにとっては大きな違いです。

だから、一流のプロ野球選手が女子の球を打てないと恥じることはないのです。

素直に女子ソフト選手のすごさをたたえればよいのです。

では、また。

　 　

第39回 硬式球と軟式球、よく曲がるのはどちらか？

硬式球vs軟式球　      

硬式球と軟式球、どちらが変化球がよく曲がるか？

子供の頃は軟式野球、高校や大学の野球部では硬式を経験し、社会人になってからの趣味の野球では再び軟式でプレー。

多くの野球愛好家がたどる王道パターンです。

そんな軟式と硬式どちらも経験してきたプレーヤーの間で、たびたび話題になるのがこのテーマです。

そこで今回は、硬式球と軟式球どちらがよく曲がるのか計算してみました。

ボールの曲がりやすさ　     

ボールによって曲がりやすいものと曲がりにくいものがありますが、それらはどのように決まるのでしょうか？

ボールの軌道を曲げる力は、ボールの進行方向と垂直な向きに作用する「揚力」です。回転によって発生するマグナス力はこの揚力の一種です。

[計算式]

揚力Lは以下の式で表されます。

L = CL×(1/2×ρ×v^2)×A　‐①

(CL:揚力係数、ρ:空気の密度、v:ボールの速度、A:ボールの断面積)

ここで、断面積は

A=π×d^2 / 4  ‐②　(d:ボールの直径)。

ボールが曲がる方向への加速度d2y/dt2は、揚力を重量で割ればよいので、以下のようになります。

d2y/dt2 = L/m   ‐③　(m:ボールの重量)

従って、③式のＬに①式を代入し、Aに②式を代入すると、以下のようになります。

　d2y/dt2 = (CL×ρ×v^2×π/8) × (d^2/m)  ‐④　。

④式から、d^2/mの値に比例して、ボールが曲がる方向への加速度d2y/dt2が大きくなることが分かります。

つまり、直径の二乗を重量で割った値(d^2/m)が、そのボールがもつ「曲がりやすさ」を表します。

（厳密には揚力係数CLもスピンパラメータSp(∝d)を介して直径dに依存しますが、ここでは省略しています。）

では、この曲がりやすさの値を硬式球、軟式球それぞれについて計算してみましょう。

 [計算結果]

硬式球

重量 : m=145[g]、直径 : d=7.4[cm]、曲がりやすさ : d^2/m=0.375[cm^2/g]

軟式球

重量 : m=138[g]、直径 : d=7.2[cm]、曲がりやすさ : d^2/m=0.376[cm^2/g]

重量および直径は上下限の中間値を使用しました。 

d^2/mの値は両者ともほぼ同じです。
つまり、硬式球と軟式球ではボールのもつ「曲がりやすさ」はほぼ同じ、ということです。

回転のかかりやすさ　      

それならば、変化球の曲がり具合はどちらも同じ、では、ありません。

ボールを横に曲げる揚力は、ボールの回転に起因するマグヌス力です。
ボールの回転数が多いほどマグヌス力は大きくなり、変化球は良く曲がります。

具体的には上記の揚力式の中に含まれている揚力係数CLが回転数により大きくなります。

硬式球と軟式球どちらの球がより回転数が大きくなりやすい、つまり、どちらの球が回転がかかりやすいか、について計算していきます。

ボールにトルクを与えるとボールは回転します。

トルクと回転数の関係は下式で表されます。
トルクTを時間積分した力積が、角運動量(I×ω )と等しくなります。

∫T dt = I×ω = I × N/(2π)

(T:トルク、I:慣性モーメント、ω:角速度、N:回転数)

そのため回転数Nは、

N = ω/(2π) = (∫T dt) / I　。

同じ力積(∫T dt)が与えられる場合、慣性モーメントIに反比例して回転数Nが大きくなります。

つまり、慣性モーメントの逆数1/Iが、そのボールの「回転のかかりやすさ」を表します。

中身が違う　　　　      

この慣性モーメントIの値が、硬式球と軟式球では違ってきます。

なぜなら、硬式球は中身が詰まっているが、軟式球は空洞だからです。

[計算式2]

球体の慣性モーメントIは以下の式で表されます。

中空

I = 2/5×m×(r^5-ri^5)/(r^3-ri^3) 　－①

(m:ボール重量、r:ボールの外半径、ri:ボールの内半径)

中実

①式にri=0を代入。

 I = 2/5×m×r^2 　－②

この式を使ってボールの回転のかかりやすさの値を硬式球、軟式球それぞれについて計算します。 

 [計算結果2]

硬式球

重量 : m=145[g]、半径 : r=7.4/2=3.69[cm]、

慣性モーメント : I=2/5×m×r^2 =791[g-cm^2]

回転のかかりやすさ : 1/I=1.26×10^-3[1/(g-cm^2)]

軟式球

重量 : m=138[g]、外半径 : r=7.2/2=3.60[cm]、内半径 : r=2.81[cm]、

慣性モーメント : I=2/5×m×(r^5-ri^5)/(r^3-ri^3) r^2 =968[g-cm^2]

回転のかかりやすさ : 1/I=1.03×10^-3[1/(g-cm^2)]

1/Ｉの値は、硬式球の方が軟式球よりも1.22倍(1.26/1.03=1.22)大きくなりました。

つまり、硬式球の方が、約1.2倍ボールに「回転がかかりやすい」、ということです。

重量が軽く、径の小さい軟式の方が回転がかかりにくいというのは意外に思われるかもしれません。

中空であるということはそれだけボールの重量がボールの中心、つまり回転軸から離れた位置に偏っていることになるため、一様に重量が分布している中実球よりも慣性モーメントが大きくなるのです。

結論　　　　　　      

というわけで、結論は以下のようになりました。

・硬式球と軟式球ではボールの持つ「曲がりやすさ」は同じ。

・硬式球の方が中実のため慣性モーメントＩが小さく、より「回転がかかりやすい」
・その結果、「硬式球の方が変化球がよく曲がる」。

*****

余談：M>A?　      

軟式野球をプレーしている人はご存知と思いますが、2018年から軟式球の仕様が変わりました。

一般向けのA号球と中学生向けのB号球は統一されてM号球に、小学生はC号球からJ号球に変わりました。

旧式のA号球よりも新型のM号球の方が、打球飛距離がアップしたことが公にされています。

一方、変化球の曲がり具合については、特に、情報公開されていません。

そのため個人の感想になりますが、私がプレーした感覚や、他の人に聞いた範囲ではA号球よりも、M号球の方が変化球の曲がりがかなり大きくなっています。

M号球の方がA号球よりもボールの直径dが少し大きいため、ボールの曲がりやすさd^2/mの値が大きくなった一方で回転のかかりにくさIの値はそこまで増加していないということがあるのかもしれません。

あるいは一部で話題になった、あのハート形の表面形状により、同じ回転数でも揚力係数CLがアップしているのかもしれません。

真相は分かりませんがM号球の開発に関わった専門家たちはA号球が硬式球より曲がらないことを事前に把握しており、硬式球に近づけるために何かしらの科学技術をM号球へ投入したのではないか、と推測されます。

では、また。

第38回 テニスのサーブと野球の球どちらが速いか？

 

テニスと野球は同じぐらい　　　　

テニスは私が野球の次に好きなスポーツです。

しかしあまりルールに詳しくないので調べていたら、あることに気が付きました。

テニスのサーブがノーバウンドで飛んでいく距離は、野球のバッテリー間とほぼ同じなのです。

テニスのサーブは自陣ベースラインの位置から打ち、相手コートのサービスラインよりも手前でワンバウンドさせます。

サービスラインを越えてしまうと”フォルト”と呼ばれる無効打になります。

テニスは２回、野球は４回　　　　

野球の場合は４球ボールでフォアボールになりますが、テニスは２回のフォルトで相手のポイントになってしまいます(ダブルフォルト)。

また、野球の場合フォアボールとホームランでは受ける損失がまるで違うため、３ボールからでもそれなりのコースを攻めます。

一方、テニスではダブルフォルトもリターンエースも損失は同じ1ポイントです。

そのため、強く打ち返えされるとしても自滅するよりはマシ、という考えで、セカンドサーブはスピードを落として確実に入れに行きます。

野球でいうところの「置きに行く」わけです。

テニスは一撃、野球は３球　　　　

野球の場合は２ストライクからストライクを取ってようやく三振になるため、最低でも3球必要になります。

そのため初球よりも追い込んでからの決め球に力を入れて投げることが多くなります。

一方、テニスではサービスエースを決めればたった1球で済んでしまいます。

そのためまだ失敗が許されるファーストサーブはフルパワーで打たれます。

世界のトップ選手ではファーストサーブの初速が200km/hを超えることもざらです。

野球の球は世界トップレベルの投手でも160km/hほどなので、テニスの球速がいかに速いかが分かります。

どっちが速い？　　　　

とはいえ、テニスの場合はサービスライン手前でワンバウンドした後さらにベースラインまで飛んでから相手選手に打ち返されるため、野球のバッテリー間よりも長い距離になります。

加えて、バウンドによる減速があること、ボールが大きさの割に軽いため空気抵抗による減速が大きいこと、を考えると、体感速度として必ずしも野球よりも速いとは言い切れない気がします。

そこで、今回はテニスのサーブと野球の投球でどちらが体感速度として速いのかを、軌道シミュレータver.3.2により計算して求めてみたいと思います。

テニスサーブの軌道計算　　　　　

体感速度とは言ったものの、人間の感覚を計算で正確に出すことは容易ではないので、ここでは放たれてから到達するまでの時間で比較することにします。

テニスはサーブが打たれてから相手のベースラインに到達するまでとして、24メートルに到達するまでの時間とします。

野球は投手がリリースしてからキャッチャーミットに収まるまでとして、19.5メートルに到達するまでの時間とします。

[計算条件]
テニスはフラットサーブで、無回転の自由落下と仮定します。

今回計算してみて初めて知ったのですが、200km/hを超えるような高速サーブでは野球のようにバックスピンをかけると角度的にどうやってもサービスラインを越えてしまいフォルトになります。

これはテニスに詳しい人にとっては常識らしいです。

また、バウンド前後で水平方向は25%、垂直方向は50%減速するとします。

野球は150km/h、2300rpmのストレートとします。

以下のような条件で計算します。

ボールに関するパラメータもテニスに合わせて変更しました。

[計算結果]

時速200km/hのテニスのサーブと、150km/hの野球の投球の軌道計算結果は以下のようになりました。

両者を重ねてプロットしてみました。

緑線がテニスコート、青線が野球のグラウンドです。

gif動画(実際のスピード）




gif動画(1/10倍スロー）


静止画(点は0.02秒ごとのボールの位置を表す)



・野球(150km/h)はリリースから捕球まで0.45秒かかる
・テニスサーブ(200km/h)はサーブを打ってからレシーブまで0.67秒かかる

200km/hでも追い抜けない　　　　　

真横から見たx-z平面における計算結果をみると、テニスのサーブは野球ボールを一度も追い抜くことができていません。

意外な結果でした。

200km/hのテニスサーブは、150km/hの野球ボールよりも初速が50km/hも速いのに追い抜くことができない理由の一つとして、野球の方がスタートラインが前であることがあります。テニスはベースライン(x=0)からサーブが打たれるのに対し、野球ではプレート(x=0)よりも1.8mも前でボールをリリースしています。

またテニスでは角度をつけて斜めに打つために、ほぼ真っ直ぐ飛んでいく野球よりも距離が長くなります。

加えて、ボールが大きさの割に軽いため空気抵抗による減速が大きいことも影響しているようです。

その結果到達時間で比べると、野球が0.45秒、テニスが0.67秒と、テニスの方が0.22秒遅くなっています。

従って、体感速度としてはテニスサーブよりも野球の方が速い、と言えそうです。

左右へ移動　　　　　

考えてみれば、テニスのレシーバーは左右に移動してボールを打ち返すだけの時間があるのに対し、野球のバッターはバッターボックスの中で移動するような時間はないのだから、今回の計算結果は当然のことです。

しかし、ではテニスのレシーブの方が野球のバッティングよりも簡単か、といえばそうは言い切れないでしょう。

打ち返すことの難しさはまた別の問題です。

ストライクゾーンの横幅よりもずっと広い範囲をテニスのレシーバーはカバーしなければなりません。

テニスのサーブを野球選手は捕れない　　

数年前に広島カープの菊池選手が、KYOKUGEN2017というテレビ番組で、テニスコートのベースラインに立ち、サーブをグラブで捕球できるのか、という企画に挑戦しました。

結果は、惨敗です。

あの名手菊池選手がまるで捕れないのです。

サーブを打っていたのは日本人トッププレイヤーですが、言い換えると世界では決してトップレベルではないような選手です。

それでも何球打っても一球も取ることができず、最後には気づかいで真正面に打ってもらってようやく捕れてめでたし、めでたし。

野球好きとしては見ていて悔しかったですが、やはりテニスのサーブはそれだけ速くてすごいのだと、改めて思い知らされました。

では、また。

　 　

第37回 第三野球部の「弾丸ボール」を再現するとどうなるか？

 

ジャイロボールの５年前　　　

ボールの回転軸が、進行方向と一致している球は「ジャイロボール」と呼ばれます。

名付け親は手塚一志さんという方で、松坂投手がメジャーに挑戦した2008年に話題となり定着しました。

彼の著書「ピッチングの正体」によれば、1995年から提唱し始めたそうです。

しかしその5年前の1990年、週刊少年マガジンで連載されていた「名門!第三野球部」に同じ回転の球が、「弾丸ボール」という呼び名で、既に登場しています。

ピストルの弾は回転している　　

甲子園でプロ注目選手を平凡な外野フライに打ち取った際、小柄な主人公の檜あすなろが投げる異常にホップする速球の秘密がその回転にある、と明らかにされます。

ピストルの弾のような回転をしているということで、その試合を中継していたアナウンサーが弾丸ボールと名付けました。

ちなみにあすなろ本人は無自覚で、普通のバックスピンの球を投げているつもりだったようです。

ピストルの内側にはライフリングというらせん状の溝が彫られており、弾丸に回転をあたえるようになっています。

なぜ回転を与えるかというと、ピストルの弾は細長い形状をしているため、横を向いてしまうと空気抵抗が増加し、軌道も曲がってしまいます。

それを防ぐために回転を与えジャイロ効果により向きを安定させています。

ジャイロ効果　　

回転をしている物体はその回転軸の向きを維持しようとする性質があります。

回転している物体は軸をずらす方向に力がかかったとき、その力の方向には倒れず、力に対して垂直な向きに回転軸が移動します。
これを物理学では「歳差運動」と言います。

物体の回転数が大きいほどこの歳差運動の動きが、ゆっくりになります。

回転している物体が倒れにくくなり、その回転軸の向きを維持しようとする性質を物理学では「ジャイロ効果」と言います。

自転車はタイヤが回っていないと不安定で横に倒れてしまいますが、勢いよく回っていると安定します。
コマも勢いよく回転していると安定して立っています。

これらはジャイロ効果の一例です。

野球のボールもおなじで、回転を与えるとボールの向きを固定することができます。

これは別にジャイロボールに限ったことではなく、カーブでもスライダーでもボールが回転している全ての球種に共通することです。

唯一、ほぼ無回転のナックルボールのみがジャイロ効果を受けません。そのためナックルボールは飛行中に縫い目の向きが変わりやすくその結果、途中で曲がる方向が変わります。

ジャイロ回転でホップするのか　　

ジャイロ回転によりボールがホップするのか、といえば、しません。

揚力が働かないため、重力により自由落下します。

むしろ、バックスピンのストレートと比べおじぎする球になります。

プロ野球では、松坂投手メジャー移籍時のジャイロボール騒ぎが起こるずっと前から「縦スラ」と呼ばれ、フォークボールと同じように落ちる変化球として普通に投げられていまし
た。

実際にジャイロボールだと間違われた松坂投手の球は「カットボール」だったと本人が語っていますが、カットボールも球速が速いのと回転軸を少し傾けバックスピン成分も与えているため縦スラほど落差がないだけで、バックスピン回転の4シームに比べるとかなりおじぎをしています。

ピストルの場合は、弾丸の初速は小拳銃でも時速1000km/hを超え、50m程度の射程距離を一瞬で通過します。

そのため重力を受ける時間が極端に短く、重力による落下量が小さいため、野球の4シームのような上向き揚力が無くてもほぼ直進します。

空気抵抗が小さい　　

第三野球の作者がフィクションとして描いた弾丸ボールも、手塚氏が現実世界での威力を提唱したジャイロボールも、共通するのは「空気抵抗が小さい」ということです。

第三野球部の作中では、プロのスカウトがスピードガンであすなろの球を計測し、初速と終速の差がわずか5キロしかないことに驚くシーンがあります。

現実世界の球では10キロ以上減速するため、本当に５キロしか減速しない球が投げられるならばかなりノビある球として認識されるはずです。

江川卓もフィクション　　　

しかし、現実には初速と終速の差がわずか5キロしかない球というのはありえません。

風洞実験や流体シミュレーションにより得られる抗力係数の値から減速がそんなに小さいことはありえないからです。

巨人で活躍した昭和の怪物・江川卓のストレートは初速と終速差は5キロしかなかった、と言われていますが、実際は機械の計測ミスの可能性が高いというのが専門家の見解です。

5年前に測定されたpitch f/xの変化量の値でさえ、最新のものと比べると明らかにずれがあります。

まして昭和時代の科学技術による測定結果はますます信頼性が低いはずです。

当時ですら怪しいと思われていたようで、次第にテレビ中継から終速表示は消されて行きました。

そのため、5キロしか減速しない弾丸ボールも現実には存在しえない、マンガの中だけのフィクションです。

弾丸ボールの軌道計算　　　

現実には存在しなくても、計算するだけならいくらでもできます。

そこで今回は、減速が5キロになるよう抗力係数の値を調整した弾丸ボールの軌道を計算し、

通常のバックスピンのストレートとのボールの飛び方の違いを比べてみます。

ちなみに弾丸ボールしか投げれなかったあすなろはプロ入り後、球種を増やすためにバックスピンストレートを持ち球の一つとして意図的に投げるようになりました。

[計算条件]

　弾丸ボール

　球速:v0=135[km/h]、リリース角度:θ=0.7度(上向き）、Φ=2.0度(一塁方向）

　リリースポイント x0=1.6m(ホーム方向)、y0=-0.4m(三塁方向)、z0=1.6m(高さ）

　ボール回転軸角度 θs=90度、Φs=0度

　ボール回転数 2000rpm(SP=0.21) : 抗力係数 CD=0.15、揚力係数CL=0.19

　バックスピンのストレート

　球速:v0=135[km/h]、リリース角度:θ=-0.5度(下向き）、Φ=2.0度(一塁方向）

　ボール回転軸角度 θs=110度、Φs=-80度

　ボール回転数 2000rpm(SP=0.21) : 抗力係数 CD=0.40、揚力係数CL=0.19

　ボール回転軸角度の定義

　θs : z軸からx-y平面に向かう角度（真上から水平に向かう角度）

　Φs : x軸からy軸に向かう角度（ホーム方向から一塁側へ向かう角度）

リリースポイントはあすなろが小柄であることを考慮した推定値です。

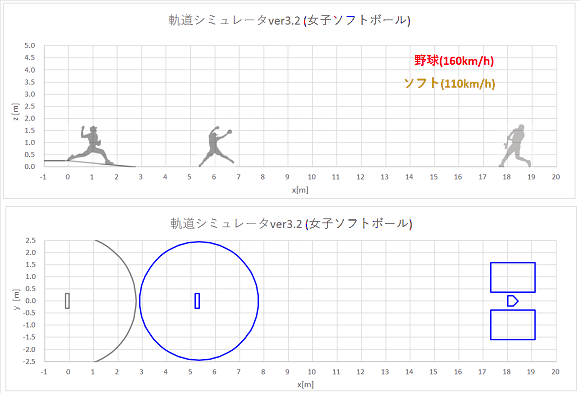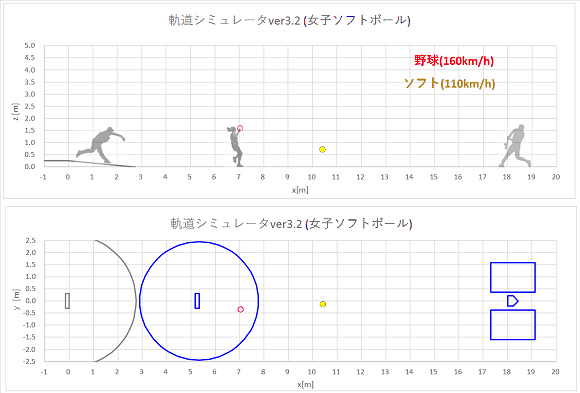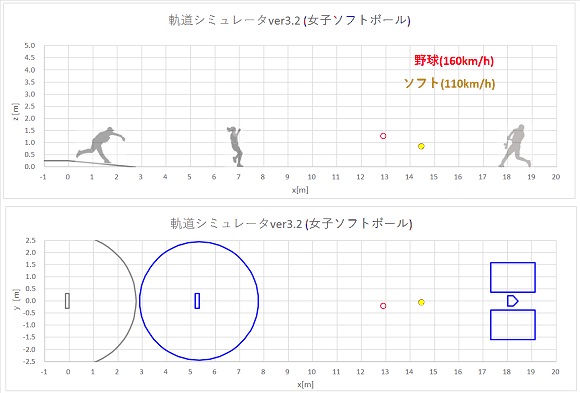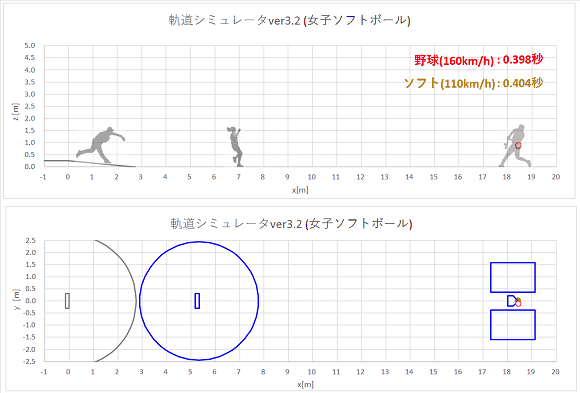
[計算結果]

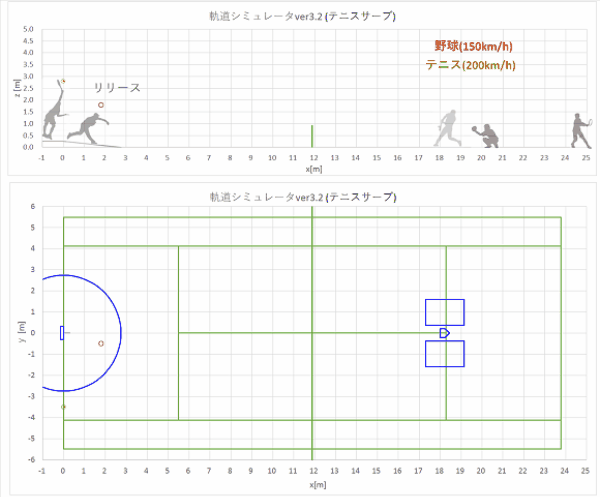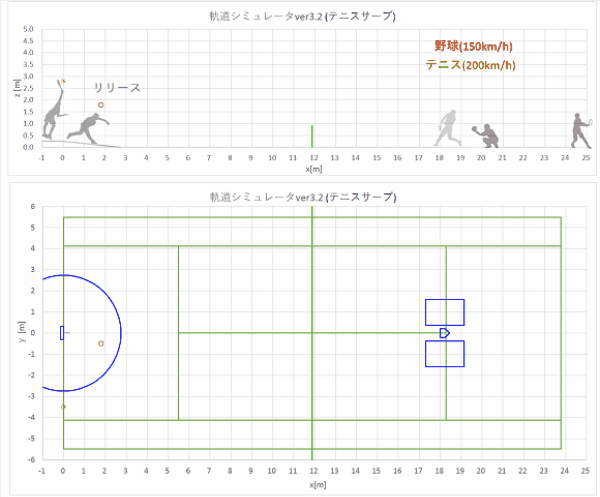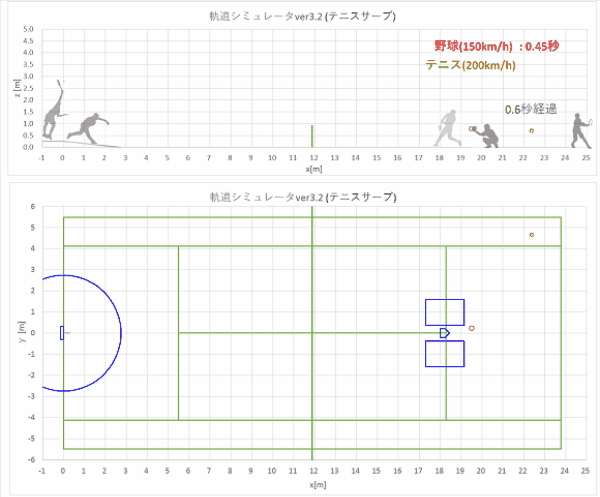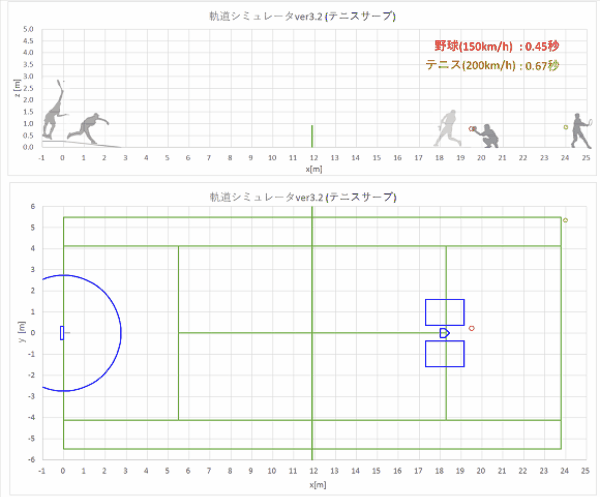
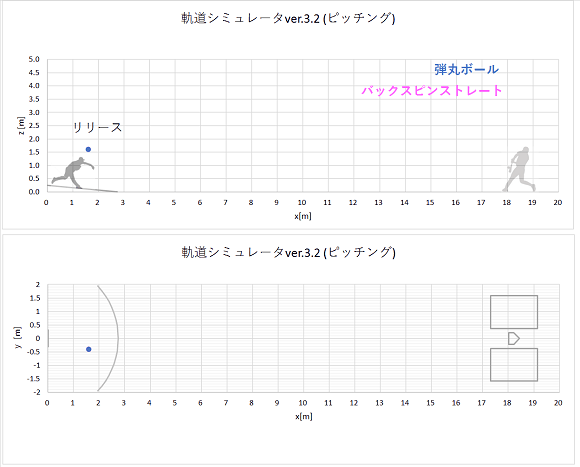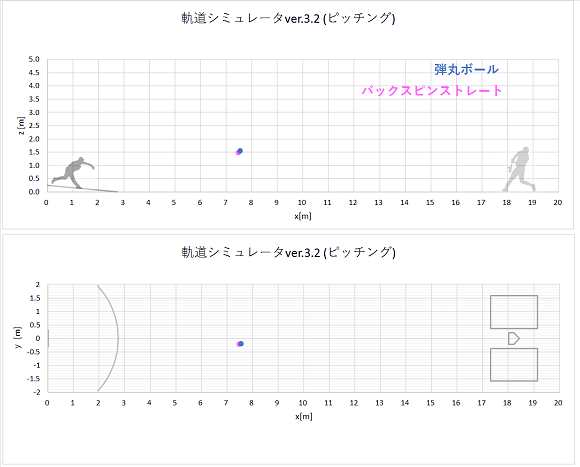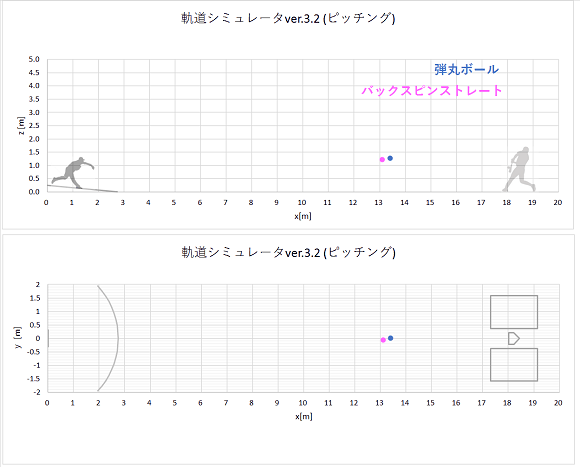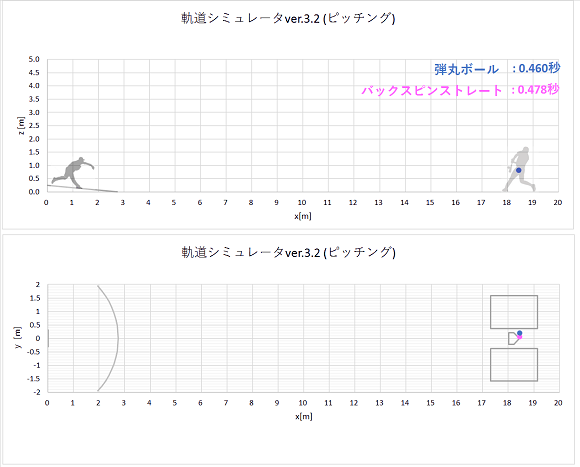
同時に同じ初速でリリースされた、弾丸ボールとバックスピンストレートの軌道計算結果をプロットすると、以下のようになりました。

上から実際の速度のgif動画、1/10倍スローのgif動画、静止画です。

リリースからホームベース(x=18.44m)到達までの時間も表示しました。

gif動画（実際の速度）

gif動画（1/10倍スロー）

静止画（点は0.02秒ごとのボール位置を表す。）

やはり、揚力の働かない弾丸ボールの方が、バックスピンストレートよりもおじぎして山なり軌道になります。

ホップする軌道にはなりません。

ただし、極端に減速の小さいこの球は人間である打者の感覚として加速してくるように感じることでしょう。

そのときこの球がホップして見えるのか、それとも沈んで見えるのかは、体験してみないことには分かりません。

野球のボールではCD=0.15という小さい抗力係数は出せないため、現実の世界で今回計算した弾丸ボールと同じ飛び方をさせるためにはボールではない、別の形状をした物体を飛ばす必要があります。

おまけのパームボール　　　

おまけとしてあすなろのもう一つの球種、パームボールも追加してみました。

デビュー戦でピッチャー返しを素手で止めて指をけがして、偶然投げられるようになった球です。

弾丸ボール、バックスピンストレートと同時に同じ角度でリリースします。

パームボールの回転についての詳細は作中で触れられていないため、115km/hで回転数500rpmのバックスピンと仮定しました。

[計算結果]

上から実際の速度のgif動画、1/10倍スローのgif動画、静止画です。

gif動画（実際の速度）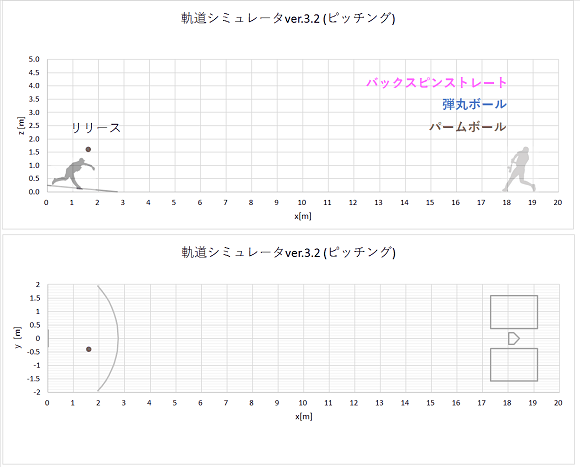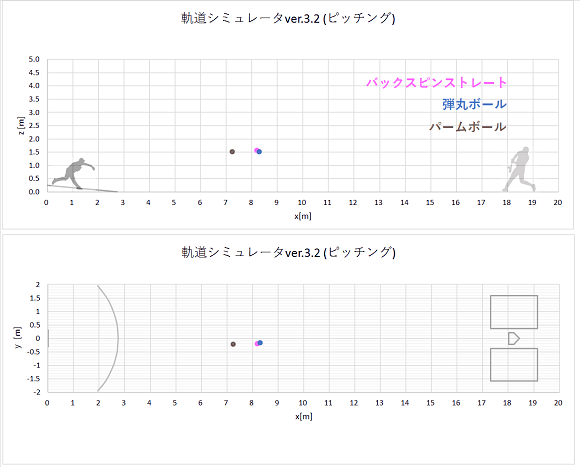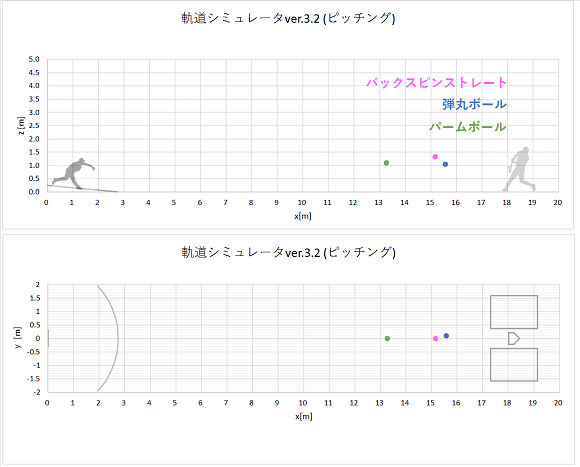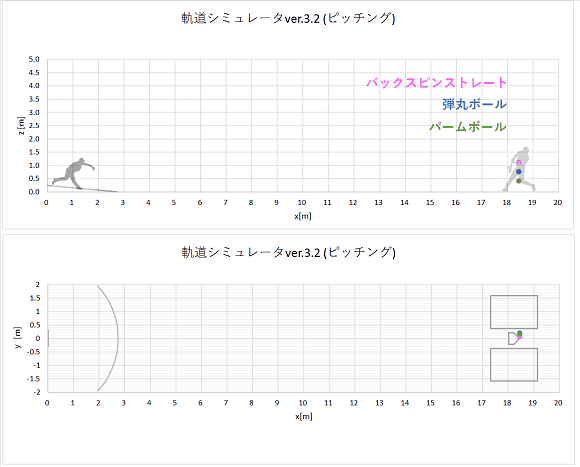




gif動画（1/10倍スロー）




静止画（点は0.02秒ごとのボール位置を表す。）

*****

第三野球部は私が子供のころ読んでいた好きな漫画です。

弾丸ボールもパームボールも真似して投げようとしていました。

一本足打法も神主打法も天秤打法も、四隅を狙った的当ても、砂浜走って鍛えるのも、小さいグラブで守備練習も、座ったままの二塁送球も、小さい靴履いて速く走ろうとするのも、みんな真似してやっていました。

どれも失敗に終わりましたが、神主打法だけは少し成功し右打ちができるようになりました。

最近リメイクされていると知って、当時を思い出して懐かしくなり筆を執った次第です。

では、また。

　 　

第36回 後攻をとれる確率

どちらが有利か？　　　　　　　

野球の試合で先攻と後攻を選べるなら、どちらにしますか？

一般的には後攻の方が有利だといわれており、人気があるようですね。

プロ野球では後攻の方が勝率が高い、という統計的な結果が出ています。

しかしながら、後攻の時は必ずホームゲームなので、ホームゲームが有利という要因も上乗せされており、純粋に後攻が有利とする根拠には弱いようです。

ホームゲームの関係ないアマチュア野球については意見が分かれますが、後攻有利説がやや優勢なようです。

唐突な問題　　　　　　　

さてここで、

唐突に数学の問題です。

[問題]

1/3を順に掛けて行くと、以下のようになります。

1/3 = 0.333333333…

1/3×1/3 = 1/9 = 0.111111111…

1/3×1/3×1/3 = 1/27 = 0.037037037…

1/3×1/3×1/3×1/3 = 1/81 =0.0123456789…

では、

これをずっと永遠に続けて行き、全部足し合せたらいくつになるでしょう？

1/3 + (1/3×1/3) + (1/3×1/3×1/3) + (1/3×1/3×1/3×1/3) +…

=(1/3)^1 + (1/3)^2 + (1/3)^3 + (1/3)^4 + …

=????

[問題おわり]

これは等比級数の和の公式を使うことで解くことができます。

※ここからしばらく数学の計算が続きます。

面倒な方は(*ﾟ▽ﾟ)ﾉまで読み飛ばしてください。

[解答]

等比級数の和の公式

Sn = a + a×r + a×r^2 +a×r^3 + … + a×r^n

= a×(1-r^n)/(1-r)

今回の場合

a=1

r=1/3

求める解x =Sn-a

なので、

x= a×(1-r^n)/(1-r)- a

    =(1-(1/3)^n)/(1-(1/3)) – 1

　ここで、

1より小さい数はかけるごとに小さくなっていくため

n＝∞のとき、(1/3)^n＝0となる。

従って

x=(1-0)/(1-(1/3)) – 1

 =3/(3-1)-1 = 3/2 - 1 = 1/2

[解答おわり]

(*ﾟ▽ﾟ)ﾉ

と言うわけで全部足し合せると1/2になります。

実はこの問題、

こんなにきちんと計算しなくても答えは分かるのです。

別解　　　　　　　　　

話を元に戻します。

先攻、後攻についてですが、高校野球の甲子園ではルールとして「審判委員立会いのもと、両校主将のジャンケンで決定される」ことになっているそうです。

では、二人でジャンケンしましょう。

一回目で勝つ確率はグー、チョキー、パーどれをだしても1/3です。

一回目はあいこで、二回目に勝つ確率は1/3×1/3です。

一、二回目ともあいこで、三回目に勝つ確率は1/3×1/3×1/3です。

気づきましたか？

何回目でもよいからとにかく勝つ確率は

1/3 + (1/3×1/3) + (1/3×1/3×1/3) +(1/3×1/3×1/3×1/3)+…

です。

そうです、

先ほどの問題と同じです。

ジャンケンで勝つ確率が1/2なのは自明ですね。

逆に言えば、ジャンケンは数学的に完全に平等であることが証明されているので、安心して勝負を運にまかせることができるのです。

パチンコや競馬などは胴元が確率を巧妙に操作しており、運任せではかならず消費者が損をするようにできています。

野球賭博もです。

気を付けてくださいね。

余談　　　　　　　　　

こんな話もあります。

 

ゆうとくんは誕生日に、魔法のケーキと魔法のナイフをもらいました。

魔法のケーキはいつまでたってもくさりません。

魔法のナイフはどんなに適当に切ってもちょうどに半分になります。

ゆうとくんはケーキが大好きなので毎日毎日、

このナイフでケーキを半分に切って一切れずつたべます。

一日目はホールのケーキを半分に切って、片方を食べて、片方をとっておきました。

二日目はとっておいたケーキを半分に切って、その片方を食べて、もう片方をとっておきました。

三日目も、四日目も同じです。

人にあげたりせず、全部ひとりでたべるつもりです。

ところで、もうひとつもらったものがあります。

それは「永遠の命」です。

さて、今から一億年後の未来、

ゆうとはどれだけたくさんのケーキを食べているでしょう？

...そう、たった一個です。

では、また。